Advent of R

2021-12-28 · Caio Lente

O Advent of Code é um Calendário do Advento desenvolvido por Eric Wastl composto por 25 pequenos exercícios de programação que vão sendo disponibilizados, um a um, entre 1º de dezembro e o Natal de cada ano.

Meu objetivo com o Advent of R foi resolver todos os problemas do Advent of Code 2021 em R e documentar o processo. Todo dia entre 01/12/2021 e 25/12/2021 eu vou resolvi o novo problema, documentei a minha solução e subi os meus scripts completos para um repositório público no GitHub.

Abaixo, cada seção representa um item de um dia do advent. Cada exercício foi individualmente resolvido no blog da Curso-R no dia correto, então todos começam com a minha opinião daquele exercício. Boas festas e bom código!

Varredura de Sonar (A)

A parte 1 do primeiro exercício do AoC envolve ler uma lista de números e ver quantas vezes os valores aumentam em relação ao anterior. Em linguagem matemática, precisamos avaliar quantas vezes $x_{i} > x_{i - 1 }$ .

Por exemplo, suponha a seguinte lista:

Nesse caso, precisamos comparar cada número com o da linha anterior e verificar se ele representa que a série aumentou, diminuiu ou manteve-se constante.

# 199 (NA)
# 200 (aumentou)
# 208 (aumentou)
# 210 (aumentou)
# 200 (diminuiu)
# 207 (aumentou)
# 240 (aumentou)
# 269 (aumentou)
# 260 (diminuiu)
# 263 (aumentou)

Tendo isso, podemos concluir que houve 7 aumentos na série exemplo e essa seria a resposta do problema.

O meu código para resolver o exercício ficou bem enxuto. Bastou ler a lista de número do arquivo disponibilizado como uma tabela e comparar seus valores com o seu dplyr::lag(); depois disso um dplyr::summarise() contou o número de TRUEs ignorando NAs.

"data-raw/01a_sonar_sweep.txt" |>
  readr::read_table(col_names = "depth") |>
  dplyr::mutate(
    prev_depth = dplyr::lag(depth),
    is_deeper = depth > prev_depth
  ) |>
  dplyr::summarise(n_deeper = sum(is_deeper, na.rm = TRUE)) |>
  dplyr::pull(n_deeper)
#> [1] 1228

Varredura de Sonar (B)

A segunda parte, entretanto, aumenta (com o perdão do trocadilho) a dificuldade. Dessa vez precisamos somar uma janela de 3 valores e comparar com a próxima janela, ou seja, verificar quantas vezes $\sum_{k = i}^{i + 2} x_{k} \geq \sum_{k = i - 1}^{i + 1} x_{k}$ .

Observe como as janelas funcionam:

# 199  A
# 200  A B
# 208  A B C
# 210    B C D
# 200  E   C D
# 207  E F   D
# 240  E F G
# 269    F G H
# 260      G H
# 263        H

Nesse exemplo precisaríamos somar os números da janela A (199, 200, 208) e testar se isso é maior que a soma dos números da janela B (200, 208, 210). Então compararíamos B com C, C com D e assim por diante.

# A: 607 (NA)
# B: 618 (aumentou)
# C: 618 (não mudou)
# D: 617 (diminuiu)
# E: 647 (aumentou)
# F: 716 (aumentou)
# G: 769 (aumentou)
# H: 792 (aumentou)

Alterando o código da primeira parte, eu criei as janelas usando dplyr::lead() e depois comparei as somas utilizando o mesmo dplyr::lag(). Mais uma vez o dplyr::summarise() contou o número de TRUEs ignorando NAs.

"data-raw/01b_sonar_sweep.txt" |>
  readr::read_table(col_names = "depth") |>
  dplyr::mutate(
    depth1 = dplyr::lead(depth, n = 1),
    depth2 = dplyr::lead(depth, n = 2),
    sum_depth = depth + depth1 + depth2,
    prev_sum_depth = dplyr::lag(sum_depth),
    is_deeper = sum_depth > prev_sum_depth
  ) |>
  dplyr::summarise(n_deeper = sum(is_deeper, na.rm = TRUE)) |>
  dplyr::pull(n_deeper)
#> [1] 1257

Mergulhe (A)

A parte 1 do segundo dia do AoC pede para lermos uma lista de comandos para um submarino e calcular a sua posição final. Os comandos possíveis são forward X (soma X à posição horizontal), up X (subtrai X da profundidade) e down X (soma X à profundidade), então precisamos fazer um dplyr::group_by(command == "forward") para que um grupo represente a posição horizontal e um represente a profundidade.

Para concluir o código, como a resposta final é a posição horizontal multiplicada pela profundidade, temos que fazer um prod() ao final:

"data-raw/02a_dive.txt" |>
  readr::read_delim(" ", col_names = c("command", "x")) |>
  dplyr::mutate(x = ifelse(command == "up", -x, x)) |>
  dplyr::group_by(command == "forward") |>
  dplyr::summarise(x = sum(x)) |>
  dplyr::summarise(x = prod(x)) |>
  dplyr::pull(x)
#> [1] 1727835

Mergulhe (B)

A parte 2 complica um pouco a nossa vida. Os mesmos comandos agora possuem outro significado:

down X aumenta a mira em X unidades
up X diminui a mira em X unidades.
forward X faz duas coisas:
- Aumenta a posição horizontal em X unidades.
- Aumenta a profundidade em X vezes a mira atual.

O meu código da primeira parte não permitiria resolver isso de forma eficiente. Minha solução foi fazer uma cumsum() da posição horizontal e uma da mira, que são as partes mais simples. Depois eu calculei a profundidade com cumsum(aim * x) (dado que a mira tinha sido calculada no passo anterior).

A saída, mais uma vez é o produto entre a posição horizontal e a profundidade. Dessa vez a resposta vai estar na última linha da tabela, então o código precisa de um tail(1).

"data-raw/02a_dive.txt" |>
  readr::read_delim(" ", col_names = c("command", "x")) |>
  dplyr::mutate(
    horizontal = ifelse(command == "forward", x, 0),
    horizontal = cumsum(horizontal),
    aim = ifelse(command == "down", x, 0),
    aim = ifelse(command == "up", -x, aim),
    aim = cumsum(aim),
    depth = ifelse(command == "forward", aim * x, 0),
    depth = cumsum(depth),
    output = horizontal * depth
  ) |>
  utils::tail(1) |>
  dplyr::pull(output)
#> [1] 1544000595

Diagnóstico Binário (A)

Na primeira parte do terceiro dia do AoC somos apresentados aos diagnósticos do submarino. Cada linha é composta por um número binário e precisamos carclular, a partir deles, os índices gama e épsilon.

Cada bit do fator gama é igual ao valor mais comum do bit correspondente na entrada, enquanto o épsilon funciona ao contrário. No exemplo acima, o primeiro bit mais comum é 1 e o segundo é 0, então o índice gama começará com 10… e o índice épsilon começará com 01…

O meu código quebra os bits da entrada com tidyr::separate() e calcula o valor mais frequente com names(sort(-table(.x)))[1] (a moda estatística). É importante lembrar que épsilon é o oposto, então eu troquei todos os bits de gama com stringr::str_replace_all(). A resposta final é a multiplicação de gama por épsilon na base decimal.

"data-raw/03a_binary_diagnostic.txt" |>
  readr::read_table(col_names = "reading") |>
  tidyr::separate(reading, paste0("B", 0:12), "") |>
  dplyr::select(-B0) |>
  dplyr::summarise_all(~names(sort(-table(.x)))[1]) |>
  tidyr::unite("gamma", dplyr::everything(), sep = "") |>
  dplyr::mutate(
    epsilon = gamma |>
      stringr::str_replace_all("0", "!") |>
      stringr::str_replace_all("1", "0") |>
      stringr::str_replace_all("!", "1") |>
      strtoi(base = 2),
    gamma = strtoi(gamma, base = 2),
    output = gamma * epsilon
  ) |>
  dplyr::pull(output)

Diagnóstico Binário (B)

O segundo item desse dia foi o mais difícil de todos, ainda mais considerando que eu tento resolver tudo em apenas uma pipeline. Usando os mesmos dados, precisamos obter a taxa de O₂ e de CO₂ do submarino, sendo que as regras são as seguintes:

Jogue fora os número que não atendem ao critério daquele gás.
Se restar apenas 1 número, essa é a taxa daquele gás.
Caso contrário, repita o processo com o próximo bit.

E quais são os critérios?

Para o oxigênio, determinamos o valor mais comum para o bit atual e jogamos fora todos os números que diferem, nessa posição, desse valor. Se 0 e 1 forem igualmente comuns, manter apenas os números com 1 no bit considerado.
Para gás carbônico, determinamos o valor menos comum para o bit atual e jogamos fora todos os números que diferem, nessa posição, desse valor. Se 0 e 1 forem igualmente comuns, manter apenas os números com 0 no bit considerado.

O primeiro passo da minha solução foi criar uma função que calcula a anti-moda de um vetor. Ela difere da função usada no item anterior somente pelo sinal de subtração, mas isso garante a ela uma propriedade importante: se 0 e 1 empatarem na contagem, ela retorna o valor que vem antes na ordem alfabética, ou seja, 0. Dessa forma a função antimode() realiza exatamente a operação que precisamos para determinar a taxa de gás carbônico.

antimode <- function(x) names(sort(table(x)))[1]

A função abaixo é uma versão recursiva do cálculo das taxas dos gases. A coluna current é só um atalho para deixar o filtro mais enxuto, pois ela não passa da do bit atual. O op(), porém, é a chave que nos permite usar a mesma função para calcular O₂ e CO₂; por padrão a função filtra os valores iguais à anti-moda, mas, com co2 = FALSE, ela filtra os valores diferentes da anti-moda, atendendo ao critério do oxigênio (incluindo o desempate)!

A última linha chama a função de novo para o próximo bit, resolvendo o cálculo.

gas <- function(df, co2 = TRUE, bit = 1) {

  # Condição de parada
  if (bit > 12 || nrow(df) == 1) return(df)

  # Escolher o operador apropriado
  if (co2) op <- `==` else op <- `!=`

  # Filtrar usando antimode() e fazer a recursão
  df |>
    dplyr::mutate(current = .data[[names(df)[bit]]]) |>
    dplyr::filter(op(current, antimode(current))) |>
    dplyr::select(-current) |>
    find_rating(co2 = co2, bit = bit + 1)
}

Só nos resta aplicar essa função na lista de números. Para tentar manter o fim do código em uma pipeline só (já que não foi possível com o resto), eu usei rep_len(list(df), 2) para duplicar a base e poder aplicar gas() e gas(co2 = FALSE) em uma linha só com purrr::map2_dfr(). O final do código deixa cada taxa em uma linha, junta os seu bits, as converte para decimal e multiplica seus valores. Essa é a saída.

"data-raw/03b_binary_diagnostic.txt" |>
  readr::read_table(col_names = "reading") |>
  tidyr::separate(reading, paste0("B", 0:12), "") |>
  dplyr::select(-B0) |>
  list() |>
  rep_len(2) |>
  purrr::map2_dfr(list(gas, \(df) gas(df, FALSE)), ~.y(.x)) |>
  tidyr::unite("reading", dplyr::everything(), sep = "") |>
  dplyr::mutate(reading = strtoi(reading, base = 2)) |>
  dplyr::summarise(output = prod(reading)) |>
  dplyr::pull(output)

Lula Gigante (A)

O quarto dia do AoC foi talvez o mais interessante até agora. Na primeira parte, precisávamos calcular a pontuação da cartela vencedora de um bingo americano: cada cartela é composta por 5 linhas e 5 colunas de números que devem ser riscados conforme eles são anunciados pelo sistema do submarino. A primeira cartela a riscar todos os números de uma linha ou coluna é a vencedora e sua pontuação é a soma de todos os números não riscados multiplicada pelo último número anunciado.

A entrada era composta por uma linha com os números anunciados em sequência e, posteriormente, todas as cartelas da platéia:

# 7,4,9,5,11,17,23,2,0,14,21,24,10,16,13,6,15,25,12,22,18,20,8,19,3,26,1
#
# 22 13 17 11  0
#  8  2 23  4 24
# 21  9 14 16  7
#  6 10  3 18  5
#  1 12 20 15 19
#
#  3 15  0  2 22
#  9 18 13 17  5
# 19  8  7 25 23
# 20 11 10 24  4
# 14 21 16 12  6
#
# 14 21 17 24  4
# 10 16 15  9 19
# 18  8 23 26 20
# 22 11 13  6  5
#  2  0 12  3  7

Eu escolhi um caminho simples para resolver o problema, apesar de o código não ter ficado tão bom assim. Primeiro eu li a sequência de números e criei uma função que transpunha uma matrix numérica e a empilhava com a original.

# Processar os números sorteados
draws <- "data-raw/04a_giant_squid.txt" |>
  readr::read_lines(n_max = 1) |>
  stringr::str_split(",") |>
  purrr::pluck(1) |>
  as.numeric()

# Converter as colunas de uma matrix para linhas e empilhar
cols_to_rows <- function(df) {
  df |>
    dplyr::select(-board, -id) |>
    as.matrix() |>
    t() |>
    tibble::as_tibble(rownames = "id") |>
    purrr::set_names("id", paste0("C", 1:5)) |>
    dplyr::mutate(board = df$board) |>
    dplyr::bind_rows(df) |>
    dplyr::relocate(board, id) |>
    purrr::set_names("id", "board", paste0("N", 1:5))
}

O objetivo de cols_to_rows() era criar uma tabela final com todas as linhas das cartelas e também todas as suas colunas; isso permitiu que eu riscasse os números sorteados aplicando dplyr::na_if() indiscriminadamente. Quando alguma linha da tabela fosse formada somente por NAs (indicando que uma linha ou coluna de alguma cartela estava completa), bastava extrair a cartela original, somar os seus valores não-NA e multiplicar o resultado pelo número sorteado mais recente. A função utilizada para isso se chamava winning_score() e operava recursivamente para poupar tempo.

# Calcular a pontuação da cartela vencedora
winning_score <- function(df, draws) {

  # Marcar o número sorteado com NA (nas linhas e colunas)
  df <- dplyr::mutate(df, dplyr::across(c(N1:N5), dplyr::na_if, draws[1]))

  # Filtrar possíveis linhas/colunas completas
  win <- dplyr::filter(df, dplyr::if_all(c(N1:N5), is.na))

  # Se houver pelo menos uma linha/coluna completa...
  if (nrow(win) > 0) {

    # Extrair a cartela vencedora, somar os não-NA e multiplicar por draws[1]
    output <- df |>
      dplyr::filter(id == win$id, stringr::str_starts(board, "R")) |>
      dplyr::select(-id, -board) |>
      purrr::flatten_dbl() |>
      sum(na.rm = TRUE) |>
      magrittr::multiply_by(draws[1])

    # Retornar a pontuação
    return(output)
  }

  # Recursão para o próximo sorteio
  winning_score(df, draws[-1])
}

# Ler cartelas, empilhas linhas com colunas e riscar usando NAs
"data-raw/04a_giant_squid.txt" |>
  readr::read_table(skip = 1, col_names = paste0("C", 1:5)) |>
  dplyr::mutate(board = (dplyr::row_number() - 1) %/% 5) |>
  dplyr::group_by(board) |>
  dplyr::mutate(id = paste0("R", 1:5)) |>
  dplyr::group_split() |>
  purrr::map_dfr(cols_to_rows) |>
  winning_score(draws)
#> [1] 33348

Lula Gigante (B)

O segundo item do problema pedia o contrário: calcular a pontuação da última cartela a ter uma linha ou coluna completa, ou seja, da cartela perdedora. Na minha solução todo o código permaneceu igual, salvo pela função winning_score(), que virou loosing_score(). A grande novidade é que, quando o programa encontrava uma cartela vencedora, ele verificava se aquela era a última. Se não fosse, ele removia aquela cartela da tabela e, se fosse, ele retornava a pontuação.

# Calcular a pontuação da cartela perdedora
loosing_score <- function(df, draws) {

  # Marcar o número sorteado com NA (nas linhas e colunas)
  df <- dplyr::mutate(df, dplyr::across(c(N1:N5), dplyr::na_if, draws[1]))

  # Filter possible complete rows or cols
  win <- dplyr::filter(df, dplyr::if_all(c(N1:N5), is.na))

  # Se houver pelo menos uma linha/coluna completa...
  if (nrow(win) > 0) {

    # Se restasse apenas uma cartela, calcular a sua pontuação
    if (length(unique(df$id)) == 1) {

      # Extrair a cartela perdedora, somar os não-NA e multiplicar por draws[1]
      output <- df |>
        dplyr::filter(stringr::str_starts(board, "R")) |>
        dplyr::select(-id, -board) |>
        purrr::flatten_dbl() |>
        sum(na.rm = TRUE) |>
        magrittr::multiply_by(draws[1])

      # Retornar a pontuação
      return(output)
    }

    # Jogar fora cartelas que já venceram
    df <- dplyr::filter(df, !id %in% win$id)
  }

  # Recursão para o próximo sorteio
  loosing_score(df, draws[-1])
}

Aventura Hidrotermal (A)

O quinto dia do AoC foi um pouco mais tranquilo do que o anterior porque eu tive ajuda da incrível Renata Hirota. Hoje tínhamos as coordenadas cartesianas do início e do fim de tubulações submarinas e o objetivo era descobrir quantos pontos do plano tinham mais de uma tubulação passando por eles. No primeiro item deveríamos considerar apenas as tubulações verticais e horizontais.

Uma entrada do tipo 1,1 -> 1,3 cobria os pontos 1,1, 1,2 e 1,3.
Uma entrada do tipo 9,7 -> 7,7 cobria os pontos 9,7, 8,7 e 7,7.

A minha ideia começava filtrando os pontos em que x1 == x2 ou y1 == y2 e expandindo as coordenadas para criar uma lista que contivesse todos os pontos pelos quais as tubulações passavam. Eu resolvi isso com o paste(x1:x2, y1:y2), pois a paste() repetiria a coordenada que não muda ao longo da coordenada que muda: paste(9:7, 7:7) := "9 7" "8 7" "7 7".

Depois disso bastava contar o números de ocorrências de cada ponto do plano, filtrar aqueles que ocorriam mais de 1 vez e contar quantos pontos restavam. Esta era a saída do problema.

"data-raw/05a_hydrothermal_venture.txt" |>
  readr::read_csv(col_names = c("x1", "y1x2", "y2")) |>
  tidyr::separate(sep = " -> ", col = "y1x2", into = c("y1", "x2")) |>
  dplyr::filter(x1 == x2 | y1 == y2) |>
  dplyr::mutate(
    dif_x = purrr::map2(x1, x2, seq),
    dif_y = purrr::map2(y1, y2, seq),
    coord = purrr::map2(dif_x, dif_y, paste)
  ) |>
  tidyr::unnest(coord) |>
  dplyr::count(coord) |>
  dplyr::filter(n > 1) |>
  nrow()
#> [1] 7142

Aventura Hidrotermal (B)

O segundo item parecia bastante mais complexo, pois agora deveríamos considerar todas as tubulações da entrada, removendo o dplyr::filter() do item anterior. Mas uma especificação do enunciado facilitou tudo: todas as linhas diagonais tinham inclinação de 45 graus.

Uma entrada do tipo 1,1 -> 3,3 cobria os pontos 1,1, 2,2 e 3,3.
Uma entrada do tipo 9,7 -> 7,9 cobria os pontos 9,7, 8,8 e 7,9.

Isso significa que a estratégia do paste() continuava funcionando! Note que paste(1:3, 1:3) := "1 1" "2 2" "3 3", então bastou tirar o dplyr::filter() que a solução estava pronta.

"data-raw/05b_hydrothermal_venture.txt" |>
  readr::read_csv(col_names = c("x1", "y1x2", "y2")) |>
  tidyr::separate(sep = " -> ", col = "y1x2", into = c("y1", "x2")) |>
  dplyr::mutate(
    dif_x = purrr::map2(x1, x2, seq),
    dif_y = purrr::map2(y1, y2, seq),
    coord = purrr::map2(dif_x, dif_y, paste)
  ) |>
  tidyr::unnest(coord) |>
  dplyr::count(coord) |>
  dplyr::filter(n > 1) |>
  nrow()
#> [1] 20012

Peixes-lanterna (A)

O dia 6 do AoC me pegou um pouco de surpresa. O primeiro item foi tranquilo de fazer: a entrada era uma lista de números que representavam os “contadores biológicos” de um cardume de peixes-lanterna e precisávamos retornar o número de peixes depois de 80 dias.

Os peixes adultos demoram 7 dias (contador vai de 6 até 0) para gerar um novo peixe bebê e um peixe bebê demora 9 dias (contador vai de 8 até 0) para gerar seu primeiro filhote.

Estado inicial   : 3,4,3,1,2
Depois de  1 dia : 2,3,2,0,1
Depois de  2 dias: 1,2,1,6,0,8
Depois de  3 dias: 0,1,0,5,6,7,8
Depois de  4 dias: 6,0,6,4,5,6,7,8,8
Depois de  5 dias: 5,6,5,3,4,5,6,7,7,8
Depois de  6 dias: 4,5,4,2,3,4,5,6,6,7
Depois de  7 dias: 3,4,3,1,2,3,4,5,5,6
Depois de  8 dias: 2,3,2,0,1,2,3,4,4,5
Depois de  9 dias: 1,2,1,6,0,1,2,3,3,4,8
Depois de 10 dias: 0,1,0,5,6,0,1,2,2,3,7,8
Depois de 11 dias: 6,0,6,4,5,6,0,1,1,2,6,7,8,8,8
Depois de 12 dias: 5,6,5,3,4,5,6,0,0,1,5,6,7,7,7,8,8
Depois de 13 dias: 4,5,4,2,3,4,5,6,6,0,4,5,6,6,6,7,7,8,8
Depois de 14 dias: 3,4,3,1,2,3,4,5,5,6,3,4,5,5,5,6,6,7,7,8
Depois de 15 dias: 2,3,2,0,1,2,3,4,4,5,2,3,4,4,4,5,5,6,6,7
Depois de 16 dias: 1,2,1,6,0,1,2,3,3,4,1,2,3,3,3,4,4,5,5,6,8
Depois de 17 dias: 0,1,0,5,6,0,1,2,2,3,0,1,2,2,2,3,3,4,4,5,7,8
Depois de 18 dias: 6,0,6,4,5,6,0,1,1,2,6,0,1,1,1,2,2,3,3,4,6,7,8,8,8,8

O meu código até que ficou bem simples. Precisei apenas de uma função que, todo dia, subtraia 1 de todos os contadores, criava 1 peixe com contador 8 para cada peixe com contador -1 e, por fim, subia todos os peixes com contador -1 para 6.

# Rodar n cíclos de reprodução do peixe-lanterna
reproduce <- function(fish, n = 80) {

  # Condição de parada
  if (n == 0) return(length(fish))

  # Reduzir contadores biológicos
  fish <- fish - 1L

  # Criar novos peixes e reiniciar contadores
  fish <- append(fish, rep_len(8L, length(fish[fish == -1L])))
  fish[fish == -1L] <- 6L

  # Recursão
  reproduce(fish, n = n - 1)
}

# Ler uma lista de peixes e reproduzir por 80 dias
"data-raw/06a_lanternfish.txt" |>
  readr::read_lines() |>
  stringr::str_split(",") |>
  purrr::pluck(1) |>
  as.integer() |>
  reproduce()
#> [1] 362666

Peixes-lanterna (B)

O segundo item do exercício não mudava essencialmente nada em relação ao primeiro. Assumindo espaço e recursos infinitos, quantos peixes teríamos depois de 256 dias?

Para resolver esse item, em teoria, seria necessário trocar apenas o valor do n por 256. Mas não foi o que aconteceu… Por causa da ineficiência do algoritmo, obter uma resposta demoraria horas e acabaria com a memória do meu computador. Foi necessário pensar em um novo método de resolver o problema.

A solução abaixo foi inspirada pela função table(). Para reduzir a exigência de espaço e não precisar iterar ao longo de um vetor com todos os peixes, eu agrupei os peixes com o mesmo contador biológico em apenas uma linha de uma tabela! Assim o programa nunca precisava lidar com mais de 9 linhas por dia, resolvendo as complicações com espaço e tempo.

# Rodar n cíclos de reprodução do peixe-lanterna
reproduce <- function(fish, n = 80) {

  # Condição de parada
  if (n == 0) return(sum(fish$n))

  # Reduzir contadores biológicos
  fish <- dplyr::mutate(fish, timer = timer - 1L)

  # Criar novos peixes
  babies <- fish |>
    dplyr::filter(timer == -1L) |>
    dplyr::mutate(timer = 8L)

  # Reiniciar contadores e recursão
  fish |>
    dplyr::bind_rows(babies) |>
    dplyr::mutate(timer = ifelse(timer == -1L, 6L, timer)) |>
    dplyr::group_by(timer) |>
    dplyr::summarise(n = sum(n)) |>
    reproduce(n = n - 1)
}

# Ler uma lista de peixes e reproduzir por 256 dias
"data-raw/06b_lanternfish.txt" |>
  readr::read_lines() |>
  stringr::str_split(",") |>
  purrr::pluck(1) |>
  as.integer() |>
  tibble::as_tibble() |>
  purrr::set_names("timer") |>
  dplyr::count(timer) |>
  reproduce(n = 256) |>
  format(scientific = FALSE)
#> [1] 1640526601595

A Traição das Baleias (A)

O dia 7 do AoC foi o mais rápido até agora. A nossa tarefa era determinar a posição horizontal na qual um exército de caranguejos deveria se alinhar, com a restrição de que deveríamos encontrar a posição que exigisse menos combustível.

Cada caranguejo estava equipado de um mini-submarino que gastava 1 unidade de combustível por unidade de deslocamento, logo o total de combustível gasto pela tropa para ir até a posição x seria simplesmente sum(abs(positions - x)). A saída era o combustível gasto para levar todos os caranguejos até a posição mais econômica.

# Ler vetor de posições iniciais
positions <- "data-raw/07a_the_treachery_of_whales.txt" |>
  readr::read_lines() |>
  stringr::str_split(",") |>
  purrr::pluck(1) |>
  as.integer()

# Iterar nas posições para encontrar a mais barata
cheapest <- Inf
for (pos in max(positions):min(positions)) {

  # Calcular o combustível gasto para a posição
  fuel <- sum(abs(positions - pos))

  # Trocar a resposta se essa posição for mais econômica
  if (fuel < cheapest) cheapest <- fuel
}

# Imprimir
cheapest
#> [1] 328318

Note que não era necessário testar nenhuma posição fora do intervalo max(positions):min(positions)! Qualquer posição fora disso seria menos econômica do que a ponta mais próxima a ela dentro do intervalo.

A Traição das Baleias (B)

O segundo item mantinha o mesmo problema, mas mudava o cálculo do gasto de combustível dos mini-submarinos: o primeiro movimento consumiria 1 unidade de combustível, o segundo consumiria 2 unidades, o terceiro consumiria 3 e assim por diante.

A única linha que muda dessa solução para a anterior é a que calcula o gasto de combustível para cada posição. Se um caranguejo estiver na posição a e quiser ir até a x, o seu consumo total será $\sum_{k = 0}^{| a - x |} k$ . Abaixo a operação sum(purrr::map_int(positions, ~sum(0:abs(.x - pos)))) faz isso para todos os caranguejos.

# Iterar nas posições para encontrar a mais barata
cheapest <- Inf
for (pos in max(positions):min(positions)) {

  # Calcular o combustível gasto para a posição
  fuel <- sum(purrr::map_int(positions, ~sum(0:abs(.x - pos))))

  # Trocar a resposta se essa posição for mais econômica
  if (fuel < cheapest) cheapest <- fuel
}

# Imprimir
cheapest
#> [1] 328318

Busca em Sete Segmentos (A)

O oitavo dia do AoC foi bastante difícil para mim. O problema começou pelo enunciado, que é longo e complexo, então realmente recomendo ler a versão original além do resumo que trago abaixo.

Dito isso, vamos lá. O problema dizia respeito a displays de sete segmentos, onde cada número é representado por um conjunto de segmentos acessos; de acordo com o diagrama abaixo, vemos que 0 é representado por abcefg, 1 é cf e assim por diante.

#   0:      1:      2:      3:      4:
#  aaaa    ....    aaaa    aaaa    ....
# b    c  .    c  .    c  .    c  b    c
# b    c  .    c  .    c  .    c  b    c
#  ....    ....    dddd    dddd    dddd
# e    f  .    f  e    .  .    f  .    f
# e    f  .    f  e    .  .    f  .    f
#  gggg    ....    gggg    gggg    ....

#   5:      6:      7:      8:      9:
#  aaaa    aaaa    aaaa    aaaa    aaaa
# b    .  b    .  .    c  b    c  b    c
# b    .  b    .  .    c  b    c  b    c
#  dddd    dddd    ....    dddd    dddd
# .    f  e    f  .    f  e    f  .    f
# .    f  e    f  .    f  e    f  .    f
#  gggg    gggg    ....    gggg    gggg

O desafio é que, no nosso submarino, todo os displays estão com os fios trocados e, para piorar, cada display tem um arranjo diferente. A entrada do problema é uma série de linhas como a abaixo: como os 10 dígitos são representados em um display específico (em qualquer ordem) e, depois da barra, 4 dígitos que precisamos decodificar.

# acedgfb cdfbe gcdfa fbcad dab cefabd cdfgeb eafb cagedb ab |
# cdfeb fcadb cdfeb cdbaf

Alguns dígitos são fáceis de identificar. Os números 1, 4, 7 e 8 usam números únicos de segmentos, então é possível perceber que, quando ab acenderam, o display estava tentando mostrar um 1. Seguindo a mesma lógica, dab é 7, eafb é 4 e acedgfb é 8.

O objetivo do primeiro item do dia 08 era contar quantas vezes os dígitos 1, 4, 7 e 8 aparecem nas saídas que devemos decodificar (lado direito da barra). A solução foi bem simples, pois bastou pivotar a tabela e filtrar as linhas que tinham stringr::str_length() igual a 2, 3, 4, ou 7.

"data-raw/08a_seven_segment_search.txt" |>
  readr::read_delim(" ", col_names = NULL) |>
  purrr::set_names(
    paste0("P", stringr::str_pad(1:10, 2, "left", "0")), "remove",
    paste0("V", stringr::str_pad(1:4, 2, "left", "0"))
  ) |>
  dplyr::select(-remove) |>
  dplyr::select(V01:V04) |>
  tidyr::pivot_longer(V01:V04, names_to = "col", values_to = "value") |>
  dplyr::filter(stringr::str_length(value) %in% c(2, 4, 3, 7)) |>
  nrow()
#> [1] 365

Busca em Sete Segmentos (B)

O verdadeiro problema veio no item 2. Aqui o exercício abandona qualquer pretexto de bondade e pede de uma vez para decodificarmos os dígitos depois da barra baseados nos 10 padrões antes da barra. A saída deveria ser a soma de todos os números de 4 dígitos decodificados.

Minha primeira tentativa de resolver o problema testava cada segmento em cada posição (essencialmente verificando todos os possíveis jeitos de embaralhar os fios) para ver em qual das configurações os padrões faziam sentido; depois seria só bater os padrões com os 4 dígitos da direita para ver quem é quem. Não preciso nem dizer que isso seria demorado demais para funcionar.

Depois de um tempo olhando para o arquivo de entrada, entretanto, me veio uma luz: talvez eu pudesse analisar a frequência com a qual cada segmento aparece nos padrões. Perceba, por exemplo, que no diagrama acima o segmento e está ligado em 4 dígitos (0, 2, 6 e 8). O fato importante é que ele é o único segmento com essa propriedade!

Partindo deste princípio, criei as seguinte regras para o código:

O único segmento que aparecer 4 vezes nos padrões corresponderá ao e;
O único segmento que aparecer 6 vezes nos padrões corresponderá ao b;
O único segmento que aparecer 9 vezes nos padrões corresponderá ao f;
No padrão com 2 segmentos acessos, aquele que não representar o e corresponderá ao c (número 1).
No padrão com 3 segmentos acessos, aquele que não representar c ou f corresponderá ao a (número 7).
No padrão com 4 segmentos acessos, aquele que não representar b, c ou f corresponderá ao d (número 4).
O segmento que ainda não tiver correspondente corresponderá ao g.

O resto do código cuidava de organizar as letras de cada dígito de modo que fosse fácil transpor as correspondências dos 10 padrões para os 4 valores das saídas.

# Decodificar uma linha da entrada
decode <- function(entry) {

  # Encontra e quebra o padrão que tenha certa str_length()
  find_by_len <- function(patterns, len) {
    patterns |>
      magrittr::extract(stringr::str_length(patterns) == len) |>
      stringr::str_split("") |>
      purrr::pluck(1)
  }

  # Frequências de referência
  ref_freq <- list(
    "a" = 8,
    "b" = 6,
    "c" = 8,
    "d" = 7,
    "e" = 4,
    "f" = 9,
    "g" = 7
  )

  # Valores de referência
  ref_val <- list(
    "abdefg" = 6,
    "abcefg" = 0,
    "cf" = 1,
    "acdfg" = 3,
    "abcdfg" = 9,
    "abcdefg" = 8,
    "bcdf" = 4,
    "acf" = 7,
    "abdfg" = 5,
    "acdeg" = 2
  )

  # Calcular frequências desta entrada
  cur_freq <- entry |>
    dplyr::select(P01:P10) |>
    purrr::flatten_chr() |>
    stringr::str_split("") |>
    purrr::flatten_chr() |>
    table()

  # Criar um dicionário para traduzir os segmentos
  dict <- list()

  # Traduzir segmentos com frequências únicas
  dict[["e"]] <- names(cur_freq[cur_freq == 4])
  dict[["b"]] <- names(cur_freq[cur_freq == 6])
  dict[["f"]] <- names(cur_freq[cur_freq == 9])

  # Extrair padrões da entrada
  patterns <- entry |>
    dplyr::select(P01:P10) |>
    purrr::flatten_chr()

  # Determinar segmento que falta do 1
  one <- find_by_len(patterns, 2)
  dict[["c"]] <- one[!one %in% purrr::flatten_chr(dict)]

  # Determinar segmento que falta do 7
  seven <- find_by_len(patterns, 3)
  dict[["a"]] <- seven[!seven %in% purrr::flatten_chr(dict)]

  # Determinar segmento que falta do 4
  four <- find_by_len(patterns, 4)
  dict[["d"]] <- four[!four %in% purrr::flatten_chr(dict)]

  # Determinar último segmento que falta
  dict[["g"]] <- names(cur_freq)[!names(cur_freq) %in% purrr::flatten_chr(dict)]

  # Traduzir segmentos dos valores de saída
  entry |>
    dplyr::select(V01:V04) |>
    purrr::flatten_chr() |>
    stringr::str_split("") |>
    purrr::map(~names(dict)[match(.x, dict)]) |>
    purrr::map(sort) |>
    purrr::map(stringr::str_c, collapse = "") |>
    purrr::map(~purrr::flatten_chr(ref_val)[match(.x, names(ref_val))]) |>
    purrr::flatten_chr() |>
    as.integer() |>
    stringr::str_c(collapse = "") |>
    as.numeric()
}

# Ler entrada, mapear decode() e somar todas os valores de saída
"data-raw/08b_seven_segment_search.txt" |>
  readr::read_delim(" ", col_names = NULL) |>
  purrr::set_names(
    paste0("P", stringr::str_pad(1:10, 2, "left", "0")), "remove",
    paste0("V", stringr::str_pad(1:4, 2, "left", "0"))
  ) |>
  dplyr::select(-remove) |>
  tibble::rowid_to_column("id") |>
  tidyr::nest(entry = c(P01:V04)) |>
  dplyr::mutate(output = purrr::map_dbl(entry, decode)) |>
  dplyr::summarise(output = sum(output)) |>
  dplyr::pull(output)
#> [1] 975706

Bacia de Fumaça (A)

O dia 9 do AoC foi desafiador, apesar de não tanto quanto o anterior. Como sempre o problema envolvia uma historinha que não contribui muito para o entendimento do enunciado, então vamos direto ao ponto: recebemos uma matriz 100x100 que representa um mapa de alturas e precisávamos encontrar todos os pontos que eram cercados (em cima, embaixo, na esquerda e na direita) por pontos mais altos. Ademais sabíamos que as alturas iam de 0 a 9 e que as fronteiras fora do mapa podiam ser todas consideradas mais altas que o resto do mapa. A resposta do problema seria o risco total de todos os pontos baixos, onde o risco de um ponto é igual à sua altura + 1.

O problema não é tão complicado, pois bastaria iterar em todos os pontos da matriz e comparar cada um com seus vizinhos. O maior dezafio era lidar com as fronteiras do mapa. Para isso, resolvi cercar toda a matriz por noves e iterar no quadrado 2:101x2:101.

# Ler o mapa de alturas e estofar as fronteiras com 9
height <- "data-raw/09a_smoke_basin.txt" |>
  readr::read_lines() |>
  stringr::str_split("") |>
  purrr::flatten_chr() |>
  as.integer() |>
  matrix(nrow = 100, ncol = 100, byrow = TRUE) |>
  rbind(rep(9, 100)) |>
  {\(m) rbind(rep(9, 100), m)}() |>
  cbind(rep(9, 102)) |>
  {\(m) cbind(rep(9, 102), m)}()

# Iterar por todos os pontos
risk <- 0
for (i in 2:101) {
  for (j in 2:101) {

    # Verificar se é um ponto baixo e somar o risco ao total
    if (
      height[i, j] < height[i - 1, j] &&
      height[i, j] < height[i + 1, j] &&
      height[i, j] < height[i, j - 1] &&
      height[i, j] < height[i, j + 1]
    ) {
      risk <- risk + height[i, j] + 1
    }
  }
}

# Imprimir
risk
#> [1] 494

Bacia de Fumaça (B)

O segundo item já era mais complicado. Considerando que os pontos com altura 9 não pertencem a nenhuma bacia, precisávamos encontrar as 3 maiores bacias no nosso mapa. Uma bacia é definida por toda uma região cercada por noves e seu tamanho é igual ao número de pontos contíguos contidos nessa área.

O diagrama abaixo não estava no enunciado, mas ele me ajudou muito a entender o que era uma bacia. Para criá-lo, eu peguei um retângulo na ponta do meu mapa e substituí todos os números menores que 9 por um ., representando assim as bacias. Cada região cercada por noves é uma bacia diferente.

# ....999.........9.9....99......9....9..........9
# ...9.9.9.......9...9..9.......9.9...99.99.9.....
# ..9.....9.9.....9...99...........999.999.9.9....
# ..9......9.9...9....999.........9..9..9.....999.
# 99..........999......9999......9..9..9.....9...9
# ...........9..9........99...9.9.......9.........
# 9..............9...9..9..9.99.9......9..........
# ...........99.9...9.99....9..99.....9...........
# ............99....9..9.......9.......9..........
# 9........99999...9....9.9....9.......999........

Minha solução começou igual à do item anterior, mas desta vez criei também uma tabela com todos os pontos do mapa. Meu objetivo era fazer uma busca em largura e remover desta tabela os pontos já explorados.

# Criar uma tabela de pontos a explorar
points <- purrr::cross2(2:101, 2:101) |>
  purrr::map(purrr::flatten_int) |>
  purrr::transpose() |>
  purrr::set_names("i", "j") |>
  tibble::as_tibble() |>
  tidyr::unnest(c(i, j))

A seguir eu criei uma função que explorava uma bacia a partir de um ponto “semente”. O primeiro passo era verificar se o ponto já tinha sido explorado e retornar 0 se sim (indicando que aquele ponto não contribuiria mais para o tamanho da bacia). Se o ponto não tivesse sido explorado, então o código o removia da tabela de pontos e verificava se ele tinha altura 9, mais uma vez retornando 0 se sim. O final da função aplicava uma recursão nos 4 vizinhos do ponto, somando os tamanhos das 4 sub-bacias encontradas mais 1 (indicando que o ponto “semente” contribuia em 1 para o tamanho total da bacia).

# Explorar uma bacia
explore <- function(a, b) {

  # Pular se o ponto já tiver sido explorado
  if (nrow(dplyr::filter(points, i == a, j == b)) == 0) return(0)

  # Marcar o ponto como explorado
  points <<- dplyr::filter(points, i != a | j != b)

  # Se a altura for 9, então ele não faz parte da bacia
  if (height[a, b] == 9) return(0)

  # Adicionar os pontos vizinhos à bacia
  return(
    explore(a - 1, b) +
    explore(a + 1, b) +
    explore(a, b - 1) +
    explore(a, b + 1) + 1
  )
}

A resposta para o item era o produto dos tamanhos das 3 maiores bacias do mapa, então o programa terminava iterando na matriz, calculando o tamanho de todas as bacias e seguindo para obter o resultado final.

# Iterar por todos os pontos
basins <- matrix(rep(0, 10404), 102, 102)
for (i in 2:101) {
  for (j in 2:101) {
    basins[i, j] <- explore(i, j)
  }
}

# Multiplicar as 3 maiores bacias
basins |>
  sort(decreasing = TRUE) |>
  magrittr::extract(1:3) |>
  prod()
#> [1] 1048128

Pontuação de Sintaxe (A)

O dia 10 do AoC pedia para que resolvessemos um clássico problema de parentização com alguns facilitadores. Em resumo, recebíamos uma string composta por parênteses e seus amigos ("(", “[”, “{”, “<”, “>”, “}”, “]”, “)”) e precisávamos identificar se o fechamento de algum deles estava errado, por exemplo, “[}”, “{()()()>”, etc. Para cada string que tivesse um fechamento ilegal recebia uma quantidade de pontos de acordo com a tabela abaixo e, finalmente, a saída do exercício era a soma de todas as pontuações.

# ): 3 pontos.
# ]: 57 pontos.
# }: 1197 pontos.
# >: 25137 pontos.

Para quem nunca viu um problema desse tipo, a solução pode ser alcançada facilmente usando uma pilha. Cada caractere que abre um bloco é colocado na pilha e, para cada caractere que fecha um bloco, removemos o elemento do topo da pilha. Se os caracteres se complementam corretamente o algoritmo segue em frente, caso contrário ele busca a pontuação na tabela e retorna.

# Correspondência de valores
scores <- list(
  ")" = 3,
  "]" = 57,
  "}" = 1197,
  ">" = 25137
)

# Calcular a pontuação por caractere ilegal em uma linha
score_ilegal <- function(line) {
  stack <- flifo::lifo()

  # Iterar na linha até um elemento não corresponder
  symbols <- stringr::str_split(line, "")[[1]]
  for (symbol in symbols) {

    # Empilhar ou desempilhar (e calcular pontuação se necessário)
    if (symbol %in% c("(", "[", "{", "<")) {
      flifo::push(stack, symbol)
    } else {
      check <- flifo::pop(stack)
      if (
        (check == "{" && symbol != "}") ||
        (check == "(" && symbol != ")") ||
        (check == "[" && symbol != "]") ||
        (check == "<" && symbol != ">")
      ) {
        return(scores[names(scores) == symbol][[1]])
      }
    }
  }

  return(0)
}

# Iterar nas linhas e calcular pontuações
"data-raw/10a_syntax_scoring.txt" |>
  readr::read_lines() |>
  purrr::map_dbl(score_ilegal) |>
  sum()
#> [1] 216297

Pontuação de Sintaxe (B)

O segundo item do problema pedia para que começássemos removendo as linhas que tinham pontuação maior que 0 (então só foi necessário filtrar isso no código, que vou omitir). Depois disso o objetivo era completar as linhas que restavam.

O fato é que as linhas restantes estavam todas com um pedaço faltando, por exemplo, “[({(<(())[]>[[{[]{<()<»” precisa ainda de “}}]])})]” para ficar correta. Usando a lógica do item anterior, só precisávamos seguir o mesmo roteiro e, ao final da linha, contar os pontos dos caracteres que ainda haviam sobrado na pilha.

Desta vez a regra de pontuação era diferente: para cada caractere faltante, precisávamos multiplicar a pontuação corrente por 5 e então somar o valor do caractere de acordo com uma nova tabelha. A resposta final era a mediana da pontuação de todoas as linhas. Enfim, o código vai a seguir:

# Ler linhas e remover corrompidas
lines <- readr::read_lines("data-raw/10b_syntax_scoring.txt")
lines <- lines[purrr::map_dbl(lines, score_ilegal) == 0]

# Correspondência de valores
scores <- list(
  "(" = 1,
  "[" = 2,
  "{" = 3,
  "<" = 4
)

# Calcular a pontuação por caractere faltante em uma linha
score_complete <- function(line) {
  stack <- flifo::lifo()

  # Iterar na linha e remover parte completa
  symbols <- stringr::str_split(line, "")[[1]]
  for (symbol in symbols) {

    # Empilhar ou desempilhar
    if (symbol %in% c("(", "[", "{", "<")) {
      flifo::push(stack, symbol)
    } else {
      flifo::pop(stack)
    }
  }

  # Iterar no resto da pilha e calcular pontos
  score <- 0
  while (flifo::size(stack) > 0) {
    check <- flifo::pop(stack)
    score <- (score * 5) + scores[names(scores) == check][[1]]
  }

  return(score)
}

# Pegar mediana das pontuações
lines |>
  purrr::map_dbl(score_complete) |>
  median()
#> [1] 2165057169

Polvo-dumbo (A)

O dia 11 do AoC foi bastante complicado e o meu código talvez tenha ficado pior ainda. As instruções eram até simples: recebemos uma matriz 10x10 com os níveis de energia de 100 polvos-dumbo e precisávamos acompanhar seus níveis de energia ao longo de 100 iterações. As regras eram as seguintes:

Primeiro, o nível de energia de cada polvo sobe em 1.
Depois, qualquer polvo com nível de energia maior que 9 emite luz (pisca). Isso aumenta o nível de energia de todos os polvos adjacentes em 1, incluindo os adjacentes diagonalmente. Se isso causar um polvo a atingir um nível de energia maior que 9, ele também pisca. Esse processo continua conforme mais polvos passam do nível de energia 9. Um polvo só pode piscar uma vez por passo e não pode subir mais nenhum nível de energia a partir daí.
Finalmente, todos os polvos que piscaram durante este passo têm seus níveis de energia ajustados para 0 (já que ele usou toda a sua energia para piscar).

Meu código seguia esse procedimento à risca e precisou de 3 loops aninhados para funcionar. O truque mais importante foi criar um clone dos polvos que marcava todos os polvos que já tinham piscado para garantir que nenhum deles ganharia mais energia durante aquele passo; este mecanismo envolvia marcar um polvo que piscava com 0 e um polvo que tinha piscado em qualquer ponto anterior do loop com -1 (para que ele não fosse contado duas vezes). O resultado final deveria ser o número de piscadas totais depois dos 100 passos.

# Ler matriz
dumbo <- "data-raw/11a_dumbo_octopus.txt" |>
  readr::read_table(col_names = FALSE) |>
  tidyr::separate(X1, paste0("C", 0:10), "") |>
  dplyr::select(-C0) |>
  dplyr::mutate_all(as.numeric) |>
  as.matrix()

# Iterar nos 100 passos
flashes <- 0
for (k in 1:100) {

  # Aumentar níveis de energia
  dumbo <- (dumbo + 1) %% 10

  # Adicionar energia aos polvos cujos vizinhos piscaram
  flag <- FALSE
  while(!flag) {

    # Contar piscadas
    flashes <- flashes + sum(dumbo == 0)

    # Adicionar energia aos polvos adjacentes a piscadas
    dumbo_ <- dumbo
    for (i in 1:10) {
      for (j in 1:10) {

        # Índices dos vizinhos
        i1 <- i - 1
        i2 <- min(i + 1, 10)
        j1 <- j - 1
        j2 <- min(j + 1, 10)

        # Adicionar energia nos índices (exceto no centro)
        if (dumbo[i, j] == 0) {
          dumbo_[i1:i2, j1:j2] <- dumbo_[i1:i2, j1:j2] + 1
          dumbo_[i, j] <- dumbo_[i, j] - 1
        }
      }
    }

    # Separar piscadas anteriores dos que piscaram na última iteração
    dumbo <- ifelse(dumbo == -1, 0, dumbo)

    # Sobrescrever as piscadas com 0 (eles não podem receber mais energia)
    dumbo <- ifelse(dumbo == 0, 0, dumbo_)

    # Verificar se o passo atual acabou
    if (!any(dumbo > 9)) {
      flag <- TRUE
    } else {

      # Prevenir piscadas antigas de serem contadas de novo
      dumbo <- ifelse(dumbo == 0, -1, dumbo)
      dumbo <- ifelse(dumbo > 9, 0, dumbo)
    }
  }
}

# Imprimir
flashes
#> [1] 1681

Polvo-dumbo (B)

Felizmente o segundo item o exercício de hoje foi bem mais simples. Eventualmente todos os polvos entram em sincronia, ou seja, passam a piscar todos juntos; o nosso objetivo era descobrir em que passo isso acontecia. A única coisa que precisei fazer com o código do item anterior foi ignorar o limite de passos e criar uma verificação para quando todos os polvos atingiam 0 de energia juntos.

# Ler matriz
dumbo <- "data-raw/11b_dumbo_octopus.txt" |>
  readr::read_table(col_names = FALSE) |>
  tidyr::separate(X1, paste0("C", 0:10), "") |>
  dplyr::select(-C0) |>
  dplyr::mutate_all(as.numeric) |>
  as.matrix()

# Iterar em 1000 passos
for (k in 1:1000) {
  print(k)

  # Aumentar níveis de energia
  dumbo <- (dumbo + 1) %% 10

  # Adicionar energia aos polvos cujos vizinhos piscaram
  flag <- FALSE
  while(!flag) {

    # Adicionar energia aos polvos adjacentes a piscadas
    dumbo_ <- dumbo
    for (i in 1:10) {
      for (j in 1:10) {

        # Índices dos vizinhos
        i1 <- i - 1
        i2 <- min(i + 1, 10)
        j1 <- j - 1
        j2 <- min(j + 1, 10)

        # Adicionar energia nos índices (exceto no centro)
        if (dumbo[i, j] == 0) {
          dumbo_[i1:i2, j1:j2] <- dumbo_[i1:i2, j1:j2] + 1
          dumbo_[i, j] <- dumbo_[i, j] - 1
        }
      }
    }

    # Separar piscadas anteriores dos que piscaram na última iteração
    dumbo <- ifelse(dumbo == -1, 0, dumbo)

    # Sobrescrever as piscadas com 0 (eles não podem receber mais energia)
    dumbo <- ifelse(dumbo == 0, 0, dumbo_)

    # Verificar se o passo atual acabou
    if (!any(dumbo > 9)) {
      flag <- TRUE
    } else {

      # Prevenir piscadas antigas de serem contadas de novo
      dumbo <- ifelse(dumbo == 0, -1, dumbo)
      dumbo <- ifelse(dumbo > 9, 0, dumbo)
    }
  }

  # Parar se todos os polvos tiverem piscado
  if (all(dumbo %in% c(0, -1))) {
    break()
  }
}

# Imprimir
k
#> [1] 276

Busca de Caminho (A)

O dia 12, juntamente com os anteriores, começou a me deixar preocupado com os próximos exercícios do Advent of Code. Aparentemente a dificuldade vai aumentando conforme o passar dos dias, mas já estou chegando no limite do meu conhecimento.

Mais uma vez temos um enunciado complicado, então leia a versão original se ficar difícil de entender aqui. Nosso objetivo esta vez era contar o número de caminhos que o nosso submarino podia tomar em um sistema de cavernas.

A entrada era uma lista de arestas nomeadas em um grafo. Os nossos caminhos deveriam sempre começar na caverna chamada “start” e terminar na chamada “end”, sendo que todas as outras eram divididas em dois grupos: grandes e pequenas. Uma caverna grande era demarcada por uma letra maiúscula e podia ser utilizada pelo nosso caminho qualquer número de vezes. Já uma caverna pequena (demarcada por uma letra minúscula), só podia ser utilizada uma vez no caminho.

Veja o exemplo abaixo. A primeira parte seria a entrada do problema, a segunda, o diagrama das cavernas e a terceira, os 10 possíveis caminhos para o nosso submarino.

# start-A
# start-b
# A-c
# A-b
# b-d
# A-end
# b-end

#     start
#     /   \
# c--A-----b--d
#     \   /
#      end

# start,A,b,A,c,A,end
# start,A,b,A,end
# start,A,b,end
# start,A,c,A,b,A,end
# start,A,c,A,b,end
# start,A,c,A,end
# start,A,end
# start,b,A,c,A,end
# start,b,A,end
# start,b,end

Minha solução envolvia uma tabela que representava todas as arestas do grafo do sistema de cavernas. A cada nova recursão, a última caverna poderia ser mantida na tabela ou removida (no caso das cavernas pequenas); toda vez que um caminho chegasse ao “end”, um contador global era incrementado.

# Contar caminhos distintos em um grafo
count <- 0
count_paths <- function(graph, path = "start") {

  # Verificar se o nó atual é "pequeno"
  cave <- tail(path, 1)
  is_small <- stringr::str_to_lower(cave) == cave

  # Condições de parada
  if (cave == "end") {count <<- count + 1; return(1)}
  if (!any(graph$orig == cave)) return(0)

  # Encontrar próximo nó do caminho
  searches <- graph |>
    dplyr::filter(orig == cave) |>
    dplyr::pull(dest) |>
    purrr::map(purrr::prepend, path)

  # Atualizar nós disponíveis
  graph <- if (is_small) dplyr::filter(graph, orig != cave) else graph

  # Iterar nos possíveis caminhos
  for (search in searches) {
    count_paths(graph, search)
  }

  # Retornar contador global
  return(count)
}

# Ler arestas do grafo e retornar conta dos caminhos
"data-raw/12a_passage_pathing.txt" |>
  readr::read_table(col_names = "path") |>
  tidyr::separate(path, c("orig", "dest"), "-") |>
  {\(d) dplyr::bind_rows(d, purrr::set_names(d, rev(names(d))))}() |>
  dplyr::filter(dest != "start", orig != "end") |>
  count_paths()
#> [1] 4792

Busca de Caminho (B)

O segundo item do problema mudava muito pouco o enunciado. Agora, ao invés de cada caverna pequena poder ser visitada apenas 1 vez, tínhamos um pequeno acréscimo de tempo. Isso queria dizer que, em cada caminho até o final do sistema de cavernas, podíamos visitar apenas 1 das cavernas pequenas até 2 vezes.

Minha solução foi criar um argumento chamado boost que indicava se já tínhamos usado o nosso excedente de tempo naquele caminho expecífico. Se não tivéssemos, poderíamos não retirar uma das cavernas pequenas da lista imediatamente. Esta estratégia funcionou, mas gerou caminhos repetidos (usando e não usando o boost), então, ao invés de contar os caminhos, passei a salvar os caminhos e contar o número de caminhos distintos no final.

# Pegar todos os caminhos distintos em um grafo
all_paths <- list()
get_paths <- function(graph, path = "start", boost = FALSE) {

  # Verificar se o nó atual é "pequeno"
  cave <- tail(path, 1)
  is_small <- stringr::str_to_lower(cave) == cave

  # Condições de parada
  if (cave == "end") {all_paths <<- append(all_paths, list(path)); return(1)}
  if (!any(graph$orig == cave)) return(0)

  # Encontrar próximo nó do caminho
  searches <- graph |>
    dplyr::filter(orig == cave) |>
    dplyr::pull(dest) |>
    purrr::map(purrr::prepend, path)

  # Atualizar nós disponíveis
  graph_ <- if (is_small) dplyr::filter(graph, orig != cave) else graph

  # Iterar nos possíveis caminhos
  for (search in searches) {
    get_paths(graph_, search, boost = boost)

    # Uma opção é não remover o nó do grafo e usar o boost
    if (!boost && is_small && cave != "start") {
      get_paths(graph, search, boost = TRUE)
    }
  }

  # Retornar lista global
  return(all_paths)
}

# Ler arestas do grafo e retornar conta dos caminhos distintos
"data-raw/12b_passage_pathing.txt" |>
  readr::read_table(col_names = "path") |>
  tidyr::separate(path, c("orig", "dest"), "-") |>
  {\(d) dplyr::bind_rows(d, purrr::set_names(d, rev(names(d))))}() |>
  dplyr::filter(dest != "start", orig != "end") |>
  get_paths() |>
  purrr::map_chr(stringr::str_c, collapse = "|") |>
  unique() |>
  length()
#> [1] 133360

Origami Transparente (A)

O dia 13 foi um belo alívio comparado com o dia anterior. Nossa missão hoje era descobrir o código de um sensor a partir de um código escrito em papel transparente. A entrada era uma série de coordenadas de pontos no papel e uma sequência de instruções de como dobrar o papel para obter o código final.

Partindo do princípio de que a matriz começava no ponto (0, 0) na esqueda superior, o primeiro item pedia para que lêssemos a nossa lista de coordenadas e contasse o número de pontos (#) visíveis depois de realizar a primeira instrução que nos era dada. Para ilustrar como as dobras ocorriam, veja os resultados de uma dobra em y = 7 e, depois, de uma dobra em x = 5:

# Papel inicial
# ...#..#..#.
# ....#......
# ...........
# #..........
# ...#....#.#
# ...........
# ...........
# ...........
# ...........
# ...........
# .#....#.##.
# ....#......
# ......#...#
# #..........
# #.#........

# Linha em y = 7
# ...#..#..#.
# ....#......
# ...........
# #..........
# ...#....#.#
# ...........
# ...........
# -----------
# ...........
# ...........
# .#....#.##.
# ....#......
# ......#...#
# #..........
# #.#........

# Resultado da primeira dobra
# #.##..#..#.
# #...#......
# ......#...#
# #...#......
# .#.#..#.###
# ...........
# ...........

# Linha em x = 5
# #.##.|#..#.
# #...#|.....
# .....|#...#
# #...#|.....
# .#.#.|#.###
# .....|.....
# .....|.....

# Resultado final
# #####
# #...#
# #...#
# #...#
# #####
# .....
# .....

O maior desafio no código em R foi arrumar todas as coordenadas e sub-matrizes para um sistema que começa em 1 e não em 0. Eu também resolvi fazer uma aposta: o primeiro item pedia para fazer apenas a primeira dobra, então eu imaginei que o segundo item pediria para fazer todas. Minha decisão, portanto, foi tentar já generalizar meu algortimo para que ele funcionasse com o mínimo de alterações possíveis para realizar várias dobras.

# Ler tabela de onde os pontos estão
dots <- "data-raw/13a_transparent_origami.txt" |>
  readr::read_lines() |>
  stringr::str_subset("^[0-9]") |>
  tibble::tibble() |>
  purrr::set_names("dot") |>
  tidyr::separate(dot, c("x", "y"), ",") |>
  dplyr::mutate_all(as.integer) |>
  dplyr::mutate_all(`+`, 1L)

# Ler instruções das dobras
instructions <- "data-raw/13a_transparent_origami.txt" |>
  readr::read_lines() |>
  stringr::str_subset("^[^0-9]") |>
  tibble::tibble() |>
  purrr::set_names("fold") |>
  tidyr::separate(fold, c("axis", "line"), "=") |>
  dplyr::mutate(
    axis = stringr::str_sub(axis, -1),
    line = as.integer(line) + 1L
  )

# Colocar os pontos no papel
paper <- matrix(FALSE, nrow = max(dots$y), ncol = max(dots$x))
for (i in seq_len(nrow(dots))) {
  paper[dots$y[i], dots$x[i]] <- TRUE
}

# Rodar apenas a primeira instrução
for (i in 1) {

  # Achar o eixo e o ponto da dobra
  axis <- instructions$axis[i]
  line <- instructions$line[i]

  # Dobras de acordo com o eixo
  if (axis == "x") {

    # Número de colunas à direita da dobra
    size <- length((line + 1):dim(paper)[2])

    # Pegar colunas à direita, invertê-las e fazer um OR com o lado esquerdo
    paper[, (line - size):(line - 1)] <-
      paper[, (line + 1):(line + size)][, size:1] |
      paper[, (line - size):(line - 1)]

    # Descartar colunas representando o papel dobrado
    paper <- paper[, 1:(line - 1)]

  } else {

    # Número de linhas abaixo da dobra
    size <- length((line + 1):dim(paper)[1])

    # Pegar linhas abaixo da dobra, invertê-las e fazer um AND com as acima
    paper[(line - size):(line - 1), ] <-
      paper[(line + 1):(line + size), ][size:1, ] |
      paper[(line - size):(line - 1), ]

    # Descartar linhas representando o papel dobrado
    paper <- paper[1:(line - 1), ]
  }
}

# Contar pontos no papel
sum(paper)
#> [1] 765

Origami Transparente (B)

E minha aposta valeu à pena! De fato o enunciado da parte 2 pedia para que realizássemos todas as dobras do nosso conjunto de instruções. No final, se tudo estivesse correto, os # e . do papel deveriam formar 8 letras maiúsculas.

A única alteração no código foi trocar a condição do for:

# Iterar por todas as instruções
for (i in seq_len(nrow(instructions)))

E, no final, também foi necessário fazer um print melhor da matriz:

# Imprimir os pontos de um jeito mais amigável
paper <- ifelse(paper, "#", ".")
for (i in seq_len(nrow(paper))) {
  cat(paper[i, ])
  cat("\n")
}
# # # # . . # # # # . # . . # . # # # # . # . . . . # # # . . . # # . . # . . # .
# # . . # . . . . # . # . # . . . . . # . # . . . . # . . # . # . . # . # . . # .
# # . . # . . . # . . # # . . . . . # . . # . . . . # . . # . # . . . . # # # # .
# # # # . . . # . . . # . # . . . # . . . # . . . . # # # . . # . # # . # . . # .
# # . # . . # . . . . # . # . . # . . . . # . . . . # . . . . # . . # . # . . # .
# # . . # . # # # # . # . . # . # # # # . # # # # . # . . . . . # # # . # . . # .

Polimerização Estendida (A)

O 14º dia do AoC foi muito demorado de resolver para mim. Apesar de ambas as soluções abaixo serem “simples”, levei horas para encontrar um jeito razoável de resolver o segundo item e, infelizmente, só consegui depois de olhar uma dica na internet que deixou tudo mais simples.

Desta vez nossa missão era estender um molde de polímero através de um conjunto de regras de reação. A primeira linha da entrada era o molde e, a partir daí, tínhamos as regras de inserção:

# NNCB
#
# CH -> B
# HH -> N
# CB -> H
# NH -> C
# HB -> C
# HC -> B
# HN -> C
# NN -> C
# BH -> H
# NC -> B
# NB -> B
# BN -> B
# BB -> N
# BC -> B
# CC -> N
# CN -> C

As regras eram fáceis de entender. Cada uma delas indicava que, quando os dois elementos da esquerda se encontravam, entre eles apareceria o elemento da direita. Uma rodada de reação envolvia estender todos os pares da cadeia polimérica; no caso do exemplo, isso transformaria NNCB em NCNBCHB.

Após 10 iterações, deveríamos contar o número de ocorrências do elemento mais comum da cadeia e subtrair dele o número de ocorrências do elemento menos comum da cadeia. Esta seria a resposta do problema.

Meu código para o primeiro item acabou seguindo o que chamamos de estratégia de força bruta. A cada iteração, eu quebrava o polímero nos seus pares de elementos e fazia um join com a tabela de regras; depois era só colar tudo em uma string só e seguir em frente. No final eu só precisava encontrar as letras mais e menos comuns da string e subtraí-las.

# Ler modelo como string
poly <- readr::read_lines("data-raw/14a_extended_polymerization.txt", n_max = 1)

# Ler regras como tabela
rules <- "data-raw/14a_extended_polymerization.txt" |>
  readr::read_table(skip = 1, col_names = FALSE) |>
  purrr::set_names("pair", "rm", "insertion") |>
  dplyr::select(-rm) |>
  dplyr::mutate(insertion = stringr::str_replace(
    pair, "(.)(.)", paste0("\\1", insertion, "\\2")
  ))

# Executar uma rodada de inserções
do_insertions <- function(poly) {
  poly |>
    stringr::str_split("") |>
    purrr::pluck(1) |>
    purrr::accumulate(~paste0(stringr::str_sub(.x, -1), .y)) |>
    utils::tail(-1) |>
    purrr::map_chr(~rules[rules$pair == .x, ]$insertion) |>
    purrr::reduce(~paste0(.x, stringr::str_sub(.y, -2))) |>
    stringr::str_c(collapse = "")
}

# Rodar do_insertions() 10 vezes e fazer el. mais comum - el. menos comum
10 |>
  seq_len() |>
  purrr::reduce(~do_insertions(.x), .init = poly) |>
  stringr::str_split("") |>
  table() |>
  {\(t) list(t[which.max(t)], t[which.min(t)])}() |>
  purrr::reduce(`-`) |>
  abs() |>
  unname()
#> [1] 2584

Polimerização Estendida (B)

O segundo item parecia suspeitamente simples, mas eu estava redondamente enganado. A única instrução era repetir o problema do primeiro item para 40 iterações ao invés de 10. Pode parecer que eu não precisaria nem mudar meu código, mas note que no primeiro item a minha cadeia polimérica só chegou a ter 19457 letras. No segundo item a cadeia chegaria a… mais de 20 trilhões.

Seria necessário mudar de estratégia e foi aí que eu empaquei. Tentei diversas formas de manter apenas o número de letras na cadeia, sem armazenar a cadeia em si, mas nada funcionava. Eu até notei que a primeira e a última letras da cadeia nunca mudavam, mas isso não me ajudou.

Depois de procurar por dicas no subreddit do AoC, finalmente achei uma boa alma que havia feito uma observação incrível:

Sempre podemos manter apenas a contagem de pares distintos na cadeia. Se tivermos, por exemplo, um par AC aparecendo n = 10 vezes na cadeia e uma regra AC -> B, então na próxima iteração podemos adicionar à nossa contagem AB e BC, cada uma aparecendo n = 10 vezes.

Até aí eu já sabia, era essencialmente o que eu fazia manualmente no item 1. O problema é que, mantendo apenas as contagens dos pares, isso repetiria a letra B duas vezes, totalizando A 10 vezes, C 10 vezes e B 20 vezes. A ideia que veio a seguir, entretanto, foi o que realmente resolveu o problema:

Se pensarmos na cadeia como um todo, todos as letras serão contadas 2 vezes, exceto pela primeira e pela última, pois elas nunca ficam no meio de uma reação. O número de ocorrências de cada letra é, portanto, n / 2, exceto pelas letras que aparecem no início e no fim, paras quais a fórmula é (n + 1) / 2.

Depois disso o item 2 podia ser solucionado facilmente.

# Registrar a primeira e a última letras da cadeia original
orig <- "data-raw/14b_extended_polymerization.txt" |>
  readr::read_lines(n_max = 1) |>
  stringr::str_replace("^(.).*?(.)$", "\\1\\2") |>
  stringr::str_split("") |>
  purrr::pluck(1)

# Ler modelo já no formato de contagem de pares
poly <- "data-raw/14b_extended_polymerization.txt" |>
  readr::read_lines(n_max = 1) |>
  stringr::str_split("") |>
  purrr::pluck(1) |>
  purrr::accumulate(~paste0(stringr::str_sub(.x, -1), .y)) |>
  utils::tail(-1) |>
  tibble::tibble() |>
  purrr::set_names("pair") |>
  dplyr::count(pair)

# Ler regras como tabela
rules <- "data-raw/14b_extended_polymerization.txt" |>
  readr::read_table(skip = 1, col_names = FALSE) |>
  purrr::set_names("pair", "rm", "insertion") |>
  dplyr::select(-rm) |>
  dplyr::mutate(insertion = stringr::str_replace(
    pair, "(.)(.)", paste0("\\1", insertion, "\\2")
  ))

# Executar uma rodada de inserções
do_insertions <- function(poly) {
  poly |>
    dplyr::left_join(rules, "pair") |>
    dplyr::mutate(
      insertion = purrr::map(insertion, stringr::str_extract, c("^..", "..$"))
    ) |>
    tidyr::unnest(insertion) |>
    dplyr::group_by(pair = insertion) |>
    dplyr::summarise(n = sum(n))
}

# Rodar do_insertions() 40 vezes e fazer el. mais comum - el. menos comum
40 |>
  seq_len() |>
  purrr::reduce(~do_insertions(.x), .init = poly) |>
  dplyr::mutate(elem = stringr::str_split(pair, "")) |>
  tidyr::unnest(elem) |>
  dplyr::group_by(elem) |>
  dplyr::summarise(n = sum(n)) |>
  dplyr::mutate(
    n = ifelse(elem %in% orig, n + 1, n),
    n = n / 2
  ) |>
  dplyr::filter(n == max(n) | n == min(n)) |>
  dplyr::pull(n) |>
  purrr::reduce(`-`) |>
  abs() |>
  format(scientific = FALSE)
#> [1] 3816397135460

Quítons (A)

No 15º dia do AoC eu demorei muito mais do que deveria. Apesar de ter entendido bem o enunciado e ter identificado rapidamente o caminho para a solução, eu empaquei na implementação do algoritmo. No final achei melhor pegar uma versão pronta do algoritmo para não perder mais horas com isso.

Novamente o enunciado envolvia um submarino, uma caverna, etc. Passar por cada ponto da caverna vinha com um certo risco que variava entre 1 e 9 e nosso objetivo era levar o submarino do ponto esquerdo superior até o ponto esquerdo inferior passando pelo caminho com menor risco total. A saída do programa deveria ser a soma do risco de todos os pontos do caminho (sem incluir o ponto de entrada, pois já começávamos nele).

A esse ponto, qualquer um que tenha aprendido sobre grafos já deve estar com o sentido aranha ativado. Esse é um problema clássico da Computação que pode ser facilmente solucionado pelo algoritmo de Dijkstra. Algumas alterações são necessárias, mas todas podem ser feitas antes de executar o algoritmo.

O passo-a-passo do código é mais ou menos o seguinte:

Marcar todos os pontos como não visitados. Criar um conjunto com todos os pontos não visitador chamado conjunto não visitado.
Atribuir a todos os pontos um risco temporário: ele deve ser 0 para o nó inicial e infinito para o resto. O risco temporário de um ponto v é o risco total do caminho de menor risco já descoberto entre v e o ponto inicial. Como no começo não conhecemos nenhum outro ponto além do inicial, todos os riscos temporários começam como infinito. Fixar o ponto inicial como o atual.
Para o ponto atual, considerar todos os seus vizinhos não vizitados e calcular os seus riscos temporários através do ponto atual. Comparar o novo risco temporário ao risco atual e atribuir o menor dos dois. Por exemplo, se o risco do ponto atual A é 6 e o seu vizinho B tem risco 2, então o risco de chegar em B por A é 6 + 2 = 8. Se o risco temporário de B até agora era maior que 8, então ele deve virar 8. Caso contrário, nada muda.
Quando já tivermos considerado todos os vizinhos não visitados do ponto atual, marcar o ponto atual como visitado e removê-lo do conjunto não visitado. Um ponto visitado nunca será checado de novo.
Se o ponto final houver sido marcado como visitado, então parar. O algoritmo terminou e o risco total do melhor caminho até o distino é igual ao risco temporário que foi atribuido ao destino.
Caso contrário, selecionar o ponto não visitado que tem o menor risco temporário e torná-lo o ponto atual. Voltar ao passo 3.

Normalmente o algoritmo de Dijkstra é aplicado em grafos nos quais os custos de cada passo do caminho são atribuídos à arestas do grafo e não aos nós, como é o nosso caso. Para resolver esse problema, temos que fazer uma certa ginástica para que os custos sejam transferidos para as arestas. Cada par de nós vizinhos ganham duas arestas direcionadas, cada uma com o risco do nó para o qual ela aponta:

# Ponto atual com seus 4 vizinhos
#   7
# 9 3 1
#   6
#
# Arestas indo para o ponto atual (todas têm risco 3)
#       o
#       3
#       ↓
# o 3 → x ← 3 o
#       ↑
#       3
#       o
#
# Arestas saindo do ponto atual (todas têm o risco do vizinho)
#       o
#       ↑
#       7
# o ← 9 x 1 → o
#       6
#       ↓
#       o

Eu queria ter de fato implementado o algoritmo de Dijkstra no R por conta própria, mas eu cometi vários erros pelo caminho (eram 7:30, não me julgue) e, para não passar a manhã toda nisso, resolvi usar o pacote cppRouting para aplicar o algoritmo.

# Ler os riscos da caverna como uma matriz
cave <- "data-raw/15a_chiton.txt" |>
  readr::read_lines() |>
  stringr::str_split("") |>
  purrr::flatten_chr() |>
  as.integer() |>
  matrix(100, 100, byrow = TRUE)

# Criar uma tabela com os custos entre vizinhos
graph <- tibble::tibble()
for (i in 1:prod(dim(cave))) {

  vals <- c()
  if (i %% 100 != 0)  vals <- append(vals, i + 1L)
  if (i %% 100 != 1)  vals <- append(vals, i - 1L)
  if (i > 100)        vals <- append(vals, i - 100L)
  if (i < 9901)       vals <- append(vals, i + 100L)

  node <- tibble::tibble(from_vertex = i, to_vertex = vals, cost = cave[vals])
  graph <- dplyr::bind_rows(graph, node)
}

# Criar grafo e executar o algoritmo de Dijkstra
path <- graph |>
  cppRouting::makegraph(directed = TRUE) |>
  cppRouting::get_path_pair(from = 1L, to = 10000L) |>
  purrr::pluck(1) |>
  as.integer()

# Calcular o risco total do caminho (subtraíndo o custo da entrada)
graph |>
  dplyr::filter(to_vertex %in% path) |>
  dplyr::group_by(to_vertex) |>
  dplyr::summarise(cost = cost[1]) |>
  dplyr::summarise(risk = sum(cost)) |>
  dplyr::pull(risk) |>
  magrittr::subtract(cave[1])
#> [1] 811

Quítons (B)

O segundo item seguia a mesma lógica de outros problemas desse ano: igual ao primeiro item, mas maior. Como eu estava usando um algoritmo bastante eficiente, não tive problema nenhum nessa parte.

Aqui descobríamos que, na verdade, a caverna era 5 vezes maior em cada dimensão (ou seja, 25 vezes mais pontos). A caverna completa era, entretanto, composta por cópias da sessão original com riscos mais elevados; para obter a versão final da caverna era necessário juntar 25 cópias da original somando um certo fator a cada cópia.

# +0 +1 +2 +3 +4
# +1 +2 +3 +4 +5
# +2 +3 +4 +5 +6
# +3 +4 +5 +6 +7
# +4 +5 +6 +7 +8

Seguindo o guia acima, vemos que o canto superior esquerdo da caverna maior era igual à sessão original e, sucessivamente, chegávamos ao canto direito inferior, que era igual à sessão original, mas o risco de cada ponto era acrescido de 8. O único detalhe é que, quando o risco de um ponto passava de 9, ele voltava para 1 (igual aos polvos-dumbo que vimos anteriormente). O resto da solução era igual.

# Criar clones da caverna, somar fator de risco e juntar
cave <- cbind(
  rbind(cave + 0L, cave + 1L, cave + 2L, cave + 3L, cave + 4L),
  rbind(cave + 1L, cave + 2L, cave + 3L, cave + 4L, cave + 5L),
  rbind(cave + 2L, cave + 3L, cave + 4L, cave + 5L, cave + 6L),
  rbind(cave + 3L, cave + 4L, cave + 5L, cave + 6L, cave + 7L),
  rbind(cave + 4L, cave + 5L, cave + 6L, cave + 7L, cave + 8L)
)

# Reduzir pontos que passaram de 9
cave[cave > 9] <- cave[cave > 9] - 9

Decodificador de Pacotes (A)

O 16º problema do AoC foi bastante diverido. O enunciado era extremamente longo e cheio de detalhes, mas consegui fazer uma implementação direta e eficiente que só não funcionou de primeira por causa de um detalhe obscuro da função strtoi().

Hoje nosso objetivos era decodificar pacotes binários. Eles chegavam ao nosso submarino em hexadecimal e, depois de convertidos para binário eles tinham as seguintes características:

Os 3 primeiros bits representavam a versão do pacote;
Os 3 bits seguintes representavam o tipo do pacote, que podia cair em dois casos:
- Se o tipo (na forma decimal) fosse igual a 4, então o pacote representaria um valor. Isso queria dizer que o resto do pacote poderia ser quebrado em pedaços de 5 bits com a seguinte configuração:
  - Se o pedaço começasse com 1, então os 4 bits a seguir eram parte do valor e deveríamos continuar lendo o pacote;
  - Se o pedaço começassem em 0, então os 4 bits a seguir eram o final do valor e poderíamos parar de ler o pacote.
- Se o tipo do pacote fosse diferente de 4, então o pacote representaria um operador. Isso queria dizer que o bit de número 7 indicava o modo do pacote:
  - Se o indicador fosse 1, então os próximos 15 bits seriam iguais à soma dos comprimentos de todos os sub-pacotes contidos naquele pacote operador;
  - Se o indicador fosse 0, então os próximos 11 bits seriam iguais ao número de sub-pacotes contidos naquele pacote operador.

Simples? Longe disso. Vejamos alguns exemplos:

# Pacote literal (valor)
# D2FE28
# 110100101111111000101000
# VVVTTTAaaaaBbbbbCcccc
#
# - VVV são a versão do pacote, 6.
# - TTT são o tipo, 4. Então este pacote carrega um valor.
# - A é 1 (continuar lendo), então aaaa são o primeiro pedaço do valor.
# - B é 1 (continuar lendo), então bbbb são o segundo pedaço do valor.
# - C é 0 (parar de ler), então cccc são o último pedaço do valor.
# - O resto são bits extras.
# - Portanto, o valor carregado por este pacote é 011111100101 = 2021.
#
# Pacote operador com indicador 0
# 38006F45291200
# 00111000000000000110111101000101001010010001001000000000
# VVVTTTILLLLLLLLLLLLLLLAAAAAAAAAAABBBBBBBBBBBBBBBB
#
# - VVV são a versão do pacote, 1.
# - TTT são o tipo, 6. Então este pacote carrega um operador.
# - I é o indicador, 0. Então este pacote tem 15 bits com os comprimentos
#   dos sub-pacotes.
# - LLLLLLLLLLLLLLL contêm a soma dos comprimentos dos sub-pacotes, 27.
# - AAAAAAAAAAA são um sub-pacote carregando um valor, 10.
# - BBBBBBBBBBBBBBBB são um sub-pacote carregando um valor, 20.
#
# Pacote operador com indicador 1
# EE00D40C823060
# 11101110000000001101010000001100100000100011000001100000
# VVVTTTILLLLLLLLLLLAAAAAAAAAAABBBBBBBBBBBCCCCCCCCCCC
# - VVV são a versão do pacote, 7.
# - TTT são o tipo, 3. Então este pacote carrega um operador.
# - I é o indicador, 1. Então este pacote tem 11 bits com os número de
#   sub-pacotes.
# - LLLLLLLLLLL contêm o número de sub-pacotes, 3.
# - AAAAAAAAAAA são um sub-pacote carregando um valor, 1.
# - BBBBBBBBBBB são um sub-pacote carregando um valor, 2.
# - CCCCCCCCCCC são um sub-pacote carregando um valor, 3.

O ponto positivo desse enunciado enorme é que conseguimos implementar os recursos necessários quase em sequência.

# Converter string hexadecimal para string binária
hex_to_bits <- function(hex) {
  hex |>
    stringr::str_split("") |>
    purrr::pluck(1) |>
    purrr::map(~paste(rev(as.integer(intToBits(strtoi(.x, 16)))))) |>
    purrr::map(magrittr::extract, 29:32) |>
    purrr::flatten_chr() |>
    stringr::str_c(collapse = "")
}

# Pegar a versão de um pacote
get_version <- function(pkt) {
  strtoi(stringr::str_sub(pkt, 1, 3), 2)
}

# Pegar o tipo de um pacote
get_type <- function(pkt) {
  strtoi(stringr::str_sub(pkt, 4, 6), 2)
}

O objetivo final deste item era parsear a hierarquia de pacotes da nossa entrada e somar as versões de todos. Minha solução envolveu, desta forma, cirar uma “classe” que podia conter a versão e o comprimento de um pacote. O comprimento era importante para descartar o número certo de bits do pacote quando tivéssemos terminado de processar um sub-pacote.

Se um pacote fosse do tipo operador, então sua “classe” também conteria todos os seus sub-pacotes como elementos sem nome. O código abaixo implementa o processamento dos dois tipos de pacotes; note como foram implementadas as “classes”:

# Pegar o valor de um pacote literal
get_literal <- function(pkt) {
  interval <- c(7, 11)

  # Iterar até o último pedaço ser encontrado
  literal <- ""
  flag <- FALSE
  while (!flag) {

    # Pegar o grupo especificado pelo intervalo
    group <- stringr::str_sub(pkt, interval[1], interval[2])
    literal <- stringr::str_c(literal, stringr::str_sub(group, 2))

    # Parar se este é o último pedaço, caso contrário somar 5 ao intervalo
    if (!as.integer(stringr::str_sub(group, 1, 1))) {
      flag <- TRUE
    } else {
      interval <- interval + 5
    }
  }

  # Retornar a "classe" que descreve o pacote
  return(list(
    version = get_version(pkt),
    len = interval[2],
    value = strtoi(literal, 2)
  ))
}

# Processar um pacote operador
get_operator <- function(pkt) {
  indicator <- stringr::str_sub(pkt, 7, 7)

  # Inicializar "classe"
  out <- list(
    version = get_version(pkt)
  )

  # Lidar com os 2 indicadores
  if (as.integer(indicator)) {

    # Pegar o número de sub-pacotes e separar a cauda do pacote
    num <- strtoi(stringr::str_sub(pkt, 8, 18), 2)
    rest <- stringr::str_sub(pkt, 19)
    out$len <- 18

    # Iterar no número de pacotes
    for (i in seq_len(num)) {

      # Processar sub-pacote
      sub <- if (get_type(rest) == 4) get_literal(rest) else get_operator(rest)
      out$len <- out$len + sub$len
      out <- c(out, list(sub))

      # Atualizar a cauda dado o compimento do último sub-pacote
      rest <- stringr::str_sub(rest, sub$len + 1)
    }
  } else {

    # Pegar o limite de comprimento dos sub-pacotes e separar a cauda
    lim <- strtoi(stringr::str_sub(pkt, 8, 22), 2)
    rest <- stringr::str_sub(pkt, 23)
    out$len <- 22

    # Iterar enquanto os sub-pacotes não tiverem passado do limite
    while (lim > 0) {

      # Processar sub-pacote
      sub <- if (get_type(rest) == 4) get_literal(rest) else get_operator(rest)
      out$len <- out$len + sub$len
      out <- c(out, list(sub))

      # Atualizar a cauda dado o compimento do último sub-pacote
      rest <- stringr::str_sub(rest, sub$len + 1)
      lim <- lim - sub$len
    }
  }

  return(out)
}

O último passo do meu código era achatar toda a estrutura de árvore que seria devolvida pelas funções acima e somar todos os comprimentos.

# Somar todas as versões do pacote representado por um hex
sum_versions <- function(hex) {

  # Pegar a árvore de pacotes representada pelo hex
  pkt <- hex_to_bits(hex)
  pkts <- if (get_type(pkt) == 4) get_literal(pkt) else get_operator(pkt)

  # Achatar árvore
  while (purrr::vec_depth(pkts) > 2) {
    pkts <- purrr::flatten(pkts)
  }

  # Somar versões
  pkts |>
    magrittr::extract(names(pkts) == "version") |>
    purrr::reduce(sum)
}

# Ler pacotes de um hex e somar versões
"data-raw/16a_packet_decoder.txt" |>
  readr::read_lines() |>
  sum_versions()
#> [1] 991

Decodificador de Pacotes (B)

O segundo item era mais ou menos o que eu já esperava. Os tipos dos pacotes tinham um significado maior, ou seja, cada sub-tipo de pacote operador indicava uma operação matemática que deveria ser aplicada no valor dos seus sub-pacotes.

A operação 0 é soma (sum()).
A operação 1 é produto (prod()).
A operação 2 é mínimo (min()).
A operação 3 é máximo (max()).
A operação 5 é maior que (>).
A operação 6 é menor que (<).
A operação 7 é igual (==).

Ou seja, se um pacote tiver a estrutura (operador + (operador * (valor 1) (valor 2)) (valor 3)), então a expressão aritmética resultante seria (1 * 2) + 3). Nosso objetivo final era calcular o valor da expressão que o nosso pacote representava. Felizmente, o meu script anterior funcionava muito bem com essa alteração!

Eu troquei o elemento version da “classe” por type (o tipo do operador) e adicionei o seguinte no final do código:

# Avaliar a árvore de pacotes
get_value <- function(tree) {

  # Funções correspondentes aos tipos
  fun <- switch(as.character(tree$type),
    "0" = sum,
    "1" = prod,
    "2" = min,
    "3" = max,
    "5" = `>`,
    "6" = `<`,
    "7" = `==`,
  )

  # Aplicar função aos sub-pacotes
  apply_fun <- function(tree) {
    tree |>
      purrr::keep(names(tree) == "") |>
      purrr::map(get_value) |>
      purrr::reduce(fun)
  }

  # Aplicar recursivamente
  if (tree$type == 4) tree$value else as.numeric(apply_fun(tree))
}

# Decodificar a expressão de um pacote hex
decode <- function(hex) {
  pkt <- hex_to_bits(hex)
  tree <- if (get_type(pkt) == 4) get_literal(pkt) else get_operator(pkt)

  get_value(tree)
}

# Ler pacotes de um hex e calcular o valor da expressão
"data-raw/16b_packet_decoder.txt" |>
  readr::read_lines() |>
  decode() |>
  format(scientific = FALSE)
#> [1] 1264485568252

P.S.: Mas isso não funcionou de primeira! Eu recebi um belo NA ao final da execução e demorei para entender a causa… No final eu descobri que a função strtoi() retorna NA quando o resultado é grande demais. A solução foi trocá-la por uma função própria:

strton <- function(x) {
  y <- as.numeric(strsplit(x, "")[[1]])
  sum(y * 2^rev((seq_along(y) - 1)))
}

Cesta de Três (A)

O 17º dia do AoC foi uma ótima quebra em relação aos últimos. O enunciado era simples de entender e a solução foi fácil de criar, tudo que eu precisava depois de uma semana cansativa.

Hoje precisávamos tentar encontrar a chave do nosso submarino em uma fossa marinha. A sonda que tínhamos a bordo podia ser arremessada a partir do ponto (0, 0) com qualquer velocidade inteira tanto no eixo x quanto no y. A entrada do problema era a posição do alvo e a saída do primeiro item deveria ser a altura máxima que podíamos arremessar a sonda de modo que ela ainda atingisse o alvo.

As regras para a aceleração da sonda a cada passo eram as seguintes:

A posição x da sonda aumenta um valor igual à sua velocidade x.
A posição y da sonda aumenta um valor igual à sua velocidade y.
Por causa do atrito, a velocidade x da sonda muda em 1 um direção a 0 (ou seja, ela diminui em 1 se a velocidade for maior que 0 e aumenta em 1 caso contrário).
Por causa da gravidade, a velocidade y da sonda diminui em 1.

O grande truque do exercício era identificar todas as velocidades possíveis da sonda e depois verificar qual o levava à maior altura. Como o alvo estava sempre abaixo e à direita do (0, 0), podíamos estabelecer os limites inferiores e superiores para as velocidades x e y:

A velocidade x necessariamente tem que ser maior que 0, já que precisamos que a sonda se mova para frente. Adicionalmente, velocidade x máxima não pode ser maior que a fronteira direita do alvo; se o alvo terminar, por exemplo, em x = 10, nunca vamos acertá-lo jogando o módulo para frente com velocidade maior que 10.
Os limites da velocidade y são mais difícil de entender. Em primeiro lugar, ela nunca pode ser menor do que a fronteira inferior do alvo (pensando na mesma lógica que usamos antes, se o alvo terminar, por exemplo, em y = -10, nunca vamos acertá-lo jogando a sonda para baixo com velocidade menor que -10). O limite superior vem do fato de que se jogarmos a sonda para cima, não importando a velocidade, ela eventualmente vai voltar a y = 0 com velocidade igual à velocidade inicial menos 1, mas com sinal negativo; sendo assim, a velocidade y máxima é igual ao valor absoluto do limite inferior do alvo.

# Velocidade inicial: (6,3)
# ..................................
# .........(3,0).#..#.(2,-1)........
# .....(4,1).#........#.(1,-2)......
# ..................................
# (5,2).#..............#.(0,-3).....
# ..................................
# ..................................
# S.(6,3)..............#.(0,-4).....
# ..................................
# ..................................
# ..................................
# .....................#.(0,-5).....
# ....................TTTTTTTTTTT...
# ....................TTTTTTTTTTT...
# ....................TTTTTTTTTTT...
# ....................TTTTTTTTTTT...
# ....................T#T(0,-6)TT...
# ..................................
# ..................................

Note no diagrama acima a simetria da trajetória no eixo y. Assim fica mais fácil entender porque, por exemplo, se o limite inferior do alvo for y = -10, então nunca podemos jogar a sonda para cima com velocidade maior que 9; ela voltará para y = 0 com velocidade -10 e acertará exatamente a fronteira de baixo do alvo.

# Ler alvo como uma tabela de coordenadas
target <- "data-raw/17a_trick_shot.txt" |>
  readr::read_lines() |>
  stringr::str_split("[=,]") |>
  purrr::pluck(1) |>
  stringr::str_subset("^[0-9-]") |>
  stringr::str_replace("\\.\\.", ":") |>
  purrr::map(~eval(parse(text = .x))) |>
  purrr::cross() |>
  purrr::transpose() |>
  purrr::set_names("x", "y") |>
  tibble::as_tibble() |>
  tidyr::unnest(c(x, y))

# Todas as possíveis combinações de velocidades x e y válidas
vels <- purrr::cross(list(
  1:max(target$x),
  min(target$y):abs(min(target$y))
))

Para calcular a altura máxima que poderíamos arremessar a sonda, eu simulei a trajetória a partir de cada um dos pares de velocidades válidas e guardei a altura máxima à qual a sonda chegava. No final da iteração, se a sonda de fato atingisse o alvo, então eu comparava a altura máxima dessa combinação com a altura máxima global e mantinha a maior.

# Verificar quais pares de velocidades funcionam e pegar a altura máxima
max_height <- 0
for (vel in vels) {

  # Posição inicial
  x_pos <- 0
  y_pos <- 0

  # Velocidades iniciais
  x_vel <- vel[[1]]
  y_vel <- vel[[2]]

  # Encontrar a altura máxima deste par de velocidades
  max_height_ <- 0
  while (y_pos >= min(target$y) && x_pos <= max(target$x)) {

    # Atualizar posições
    x_pos <- x_pos + x_vel
    y_pos <- y_pos + y_vel

    # Atualizar altura máxima local
    if (y_pos > max_height_) max_height_ <- y_pos

    # Se o par de fato leva ao alvo, atualizar altura máxima global
    if (x_pos %in% target$x && y_pos %in% target$y) {
      if (max_height_ > max_height) max_height <- max_height_
    }

    # Atualizar velocidades
    x_vel <- if (x_vel > 0) x_vel - 1 else 0
    y_vel <- y_vel - 1
  }
}

# Retornar a altura máxima global
max_height
#> [1] 4753

Cesta de Três (B)

Chegando no item 2, eu percebi que tinha dado muita sorte. O enunciado aqui pedia para encontrarmos o número de velocidades iniciais da sonda que a faziam chegar ao alvo. Meu código anterior já encontrava todos os pares válidos, mas utilizava isso para atualizar a altura máxima; só era necessário trocar a variável sendo atualizada dentro do while.

# Verificar pares de velocidades que funcionam e contá-los
n_works <- 0
for (vel in vels) {

  # Posição inicial
  x_pos <- 0
  y_pos <- 0

  # Velocidades iniciais
  x_vel <- vel[[1]]
  y_vel <- vel[[2]]

  # Encontrar a altura máxima deste par de velocidades
  max_height_ <- 0
  while (y_pos >= min(target$y) && x_pos <= max(target$x)) {

    # Atualizar posições
    x_pos <- x_pos + x_vel
    y_pos <- y_pos + y_vel

    # Se o par de fato leva ao alvo, atualizar contador
    if (x_pos %in% target$x && y_pos %in% target$y) {
      n_works <- n_works + 1
      break
    }

    # Atualizar velocidades
    x_vel <- if (x_vel > 0) x_vel - 1 else 0
    y_vel <- y_vel - 1
  }
}

# Retornar número de velocidades que funcionam
n_works

Peixe-Caracol (A)

Chegou o dia 18 do AoC e mais uma vez o problema não foi muito difícil apesar do enunciado monstruoso. Uma coisa que notei hoje é que havia vários caminhos para resolver o exercício que pareciam igualmente razoáveis. No final eu decidi usar regex, uma das melhores e mais temidas funcionalidades de qualquer linguagem de programação.

O enunciado pedia para aprendermos a fazer somas usando os números dos peixes-caracol… A primeira característica desse sistema aritmético é que um número é representado por pares de elementos na forma [x,y], que podem ser números normais ou outros pares; por exemplo [[1,2],3]. Além disso, há duas limitações para os números: nunca pode haver um par dentro de 4 ou mais pares e nenhum número normal pode ser maior que 9.

A soma dos peixes-caracol coloca cada um dos dois números como elementos de um novo par. Se o primeiro número for [a,b] e o segundo [x,y], então a soma deles é [[a,b],[x,y]]. Obviamente isso pode criar um número que viola a as limitações acima, então precisamos aplicar as regras da explosão e da quebra. Abaixo eu descrevo as regras e as funções que criei para implementar cada uma:

A regra da explosão sempre vem primeiro e ela deve ser aplicada o maior número possível de vezes antes de partirmos para a regra da quebra.

# Exemplo:
# [[6,[5,[4,[3,2]]]],1]
#
# Passos da explosão:
# 1. Encontrar o primeiro par simples que está dentro de 4 ou mais pares
# [3,2]
#
# 2. Denominar as partes do par com x e y:
# [x,y] = [3,2]
#
# 3. Somar x ao número normal mais próximo à esquerda (se houver)
# [[6,[5,[4 + 3,[3,2]]]],1]
# [[6,[5,[7,[3,2]]]],1]
#
# 4. Somar y ao número normal mais próximo à direita (se houver)
# [[6,[5,[7,[3,2]]]],1 + 2]
# [[6,[5,[7,[3,2]]]],3]
#
# 5. Substituir o par por 0
# [[6,[5,[7,0]]],3]

# Encontrar posição de um par que precisa ser explodido
find_explode <- function(num) {
  chrs <- stringr::str_split(num, "")[[1]]

  # Iterar nos caracteres para encontrar um par profundo demais
  counter <- 0
  for (i in seq_along(chrs)) {
    if (chrs[i] == "[") {
      counter <- counter + 1
    } else if (chrs[i] == "]") {
      counter <- counter - 1

      # Se o par for profundo demais, retornar
      if (counter >= 4) {

        # Encontrar o começo do par
        len <- num |>
          stringr::str_sub(end = i) |>
          stringr::str_extract("\\[[^\\[]*?$") |>
          stringr::str_length() |>
          magrittr::subtract(1)

        # Retornar "coordenadas" do par
        return(c(i - len, i))
      }
    }
  }

  # Se não ouver par para explodir, returnar NULL
  return(NULL)
}

# Aplicar o algoritmo da explosão
explode <- function(num) {

  # Encontrar um par para explodir
  pos <- find_explode(num)

  # Se não houver par, retornar o número
  if (is.null(pos)) return(num)

  # Extrair números normais do par
  pair <- num |>
    stringr::str_sub(pos[1], pos[2]) |>
    stringr::str_extract_all("[0-9]+") |>
    purrr::pluck(1) |>
    as.numeric()

  # Pegar a parte esquerda do número (até o par que vai explodir)
  lhs <- stringr::str_sub(num, end = pos[1] - 1)

  # Encontrar o número normal mais próximo de pair[1] e somar
  left_num <- lhs |>
    stringr::str_extract("[0-9]+(?=[^0-9]+$)") |>
    as.numeric() |>
    magrittr::add(pair[1])

  # Pegar a parte direita do número (a partir do par que vai explodir)
  rhs <- stringr::str_sub(num, pos[2] + 1)

  # Encontrar o número normal mais próximo de pair[2] e somar
  right_num <- rhs |>
    stringr::str_extract("^[^0-9]+[0-9]+") |>
    stringr::str_remove("^[^0-9]+") |>
    as.numeric() |>
    magrittr::add(pair[2])

  # Substituir os números normais que mudamos
  lhs <- stringr::str_replace(lhs, "[0-9]+([^0-9]+)$", paste0(left_num, "\\1"))
  rhs <- stringr::str_replace(rhs, "^([^0-9]+)[0-9]+", paste0("\\1", right_num))

  # Colar as partes esquerda e direita de volta
  return(paste0(lhs, "0", rhs))
}

Se não houver mais como aplicar a explosão, então podemos fazer uma quebra e voltar para o começo do algoritmo: aplicar quantas explosões forem possíveis e depois tentar uma quebra. Quando nenhuma regra puder ser aplicada, então encontramos o resultado da soma.

# Exemplo:
# [11,1]
#
# Passos da quebra:
# 1. Encontrar o primeiro número normal maior que 9
# 11
#
# 2. Criar um novo par onde o elemento da esquerda é o número dividido por 2
#    arredondado para baixo e o elemento da direita é o número dividido por 2
#    arredondado para cima.
# [5,6]
#
# 3. Substituir o número normal pelo par criado
# [[5,6],1]

# Aplicar o algoritmo da quebra
split <- function(num) {

  # Verificar se algo precisa ser quebrado e retornar o número se não
  if (!stringr::str_detect(num, "[0-9]{2,}")) return(num)

  # Criar um par a partir das metades do primeiro número normal > 9
  pair <- num |>
    stringr::str_extract("[0-9]{2,}") |>
    as.numeric() |>
    {\(n) paste0("[", floor(n / 2), ",", ceiling(n / 2), "]")}()

  # Substituir o número normal pelo par criado
  stringr::str_replace(num, "[0-9]{2,}", pair)
}

Agora que sabemos como explodir e qubrar, podemos implementar o algoritmo completo da soma dos peixes-caracol. Notem o next no loop; ele é essencial por causa da exigência de aplicarmos a explosão quantas vezes forem necessárias.

# Soma dos peixes-caracol
snailfish_sum <- function(num1, num2) {

  # Juntar números como elementos de um novo par
  num <- paste0("[", num1, ",", num2, "]")

  # Aplicar explosão e quebra até o número não mudar mais
  num_ <- ""
  while (num_ != num) {
    num_ <- num

    # Explodir e, se o número tiver mudado, voltar
    num <- explode(num)
    if (num_ != num) next

    # Qubrar
    num <- split(num)
  }

  return(num)
}

Mas o enunciado não pedia para simplesmente implementarmos a soma dos peixes-caracol… A resposta final deveria ser a magnitude do número obtido a partir de somas sucessivas. Essencialmente, a nossa entrada era uma sequência de números A, B, C, D, etc. e devíamos calcular (((A + B) + C) + D) + .... Já a magnitude de um número envolve outro algoritmo; a magnitude de um [x,y] qualquer é 3*x + 2*y, mas devemos aplicar isso recursivamente, entrando nas camadas mais profundas do número e voltando para a superfície.

# Fazer uma rodada do algoritmo da magnitude
get_one_magnitude <- function(num) {

  # Pegar a magnitude do par mais à esquerda
  val <- num |>
    stringr::str_extract("\\[[^\\[\\]]+\\]") |>
    stringr::str_extract_all("[0-9]+") |>
    purrr::pluck(1) |>
    as.numeric() |>
    {\(n) 3 * n[1] + 2 * n[2]}() |>
    as.character()

  # Trocar o par pela sua magnitude
  stringr::str_replace(num, "\\[[^\\[\\]]+\\]", val)
}

# Aplicar o algoritmo completo da magnitude
get_magnitude <- function(num) {

  # Enquanto ainda houver pares, fazer uma rodada do cálculo
  while (stringr::str_detect(num, "\\[")) {
    num <- get_one_magnitude(num)
  }

  # Retornar magnitude convertida para um valor numérico
  return(as.numeric(num))
}

Enfim, depois de uma parede de texto e uma parede de código, podemos finalmente juntar tudo na solução do primeiro item.

# Reduce list of numbers with snalfish addition and get magnitude
"data-raw/18a_snailfish.txt" |>
  readr::read_lines() |>
  purrr::reduce(snailfish_sum) |>
  get_magnitude()
#> [1] 4124

Peixes-Caracol (B)

Em um ato de bondade, o autor do Advent of Code fez um item 2 bem simples. Dados todos os números A, B, C, D, etc. que recebemos como entrada, precisávamos combinar todos para encontrar a maior magnitude possível. Minha solução foi gerar todas as somas possíveis (A + B, B + A, A + C, C + A, etc., notando que A + B != B + A) e simplesmente calcular a magnitude de todas. A resposta do item devia ser justamente essa maior magnitude possível.

# Cruzar os números consigo mesmos e somar toda combinação
"data-raw/18b_snailfish.txt" |>
  readr::read_lines() |>
  {\(ns) list(ns, ns)}() |>
  purrr::cross(`==`) |>
  purrr::map_dbl(~get_magnitude(snailfish_sum(.x[[1]], .x[[2]]))) |>
  max()
#> [1] 4673

Detectores de Sinalizadores (A)

Neville Chamberlain tem uma frase que eu gosto muito: “na guerra não há vencedores, todos são perdedores.” É assim que eu me senti com o dia 19 do AoC. No total eu demorei mais de 6 horas de programação intensa para resolver o problema de hoje. Joguei meu código fora múltiplas vezes, quase desisti, mas no final perseverei. Não acho que eu tenha resolvido o problema; assim como Chamberlain, acredito que o problema só perdeu antes.

Por esse motivo, o post de hoje vai ser um pouco diferente. Em primeiro lugar, é impossível resumir as mais de 400 linhas do enunciado de forma efetiva e, em segundo, explicar o raciocínio por trás da minha solução seria tão exaustivo quanto. Sendo assim, vou fazer um super resumo do enunciado e deixar a explicação do código a cargo dos comentários. Quem sabe um dia eu não revisito esse exercício para dar um passo-a-passo melhor.

O grosso da pergunta é o seguinte: temos 36 detectores e uma série de sinalizadores espalhados pelo oceano em posições fixas. A entrada são as coordenadas dos sinalizadores que são vistos por cada detector relativas à posição desse detector. Cada detector também pode estar em uma de 24 orientações (olhando para +x com o topo apontado para +y, olhando para -y com o topo apontado para +z, etc.). Se dois detectores tiverem uma intersecção entre os seus cubos de detecção, então deve haver pelo menos 12 sinalizadores nesse volume. A pergunta pede para calcularmos o número de sinalizadores que estão nessa região do mar.

# Converter c(x,y,z) para "x,y,z"
vec_to_str <- function(vec) {
  stringr::str_c(vec, collapse = ",")
}

# Converter "x,y,z" para c(x,y,z)
str_to_vec <- function(str) {
  as.integer(stringr::str_split(str, ",")[[1]])
}

# Atalho para escolhe(n,2) de uma lista
choose_pairs <- function(l) {
  seq_along(l) |>
    list(seq_along(l)) |>
    purrr::cross(`==`) |>
    purrr::transpose() |>
    purrr::map(purrr::flatten_int) |>
    purrr::set_names("a", "b") |>
    dplyr::as_tibble() |>
    dplyr::rowwise() |>
    dplyr::mutate(ordered = paste0(sort(c(a, b)), collapse = ",")) |>
    dplyr::group_by(ordered) |>
    dplyr::slice_head(n = 1) |>
    dplyr::ungroup() |>
    dplyr::select(-ordered) |>
    dplyr::mutate(
      a = purrr::map(a, ~l[[.x]]),
      b = purrr::map(b, ~l[[.x]])
    )
}

# Aplicar todas as rotações de um ponto
apply_rotations <- function(point) {
  rotations <- list(
    list(c(-1, 0, 0), c(0, -1, 0), c(0, 0, 1)),
    list(c(-1, 0, 0), c(0, 0, -1), c(0, -1, 0)),
    list(c(-1, 0, 0), c(0, 0, 1), c(0, 1, 0)),
    list(c(-1, 0, 0), c(0, 1, 0), c(0, 0, -1)),
    list(c(0, -1, 0), c(-1, 0, 0), c(0, 0, -1)),
    list(c(0, -1, 0), c(0, 0, -1), c(1, 0, 0)),
    list(c(0, -1, 0), c(0, 0, 1), c(-1, 0, 0)),
    list(c(0, -1, 0), c(1, 0, 0), c(0, 0, 1)),
    list(c(0, 0, -1), c(-1, 0, 0), c(0, 1, 0)),
    list(c(0, 0, -1), c(0, -1, 0), c(-1, 0, 0)),
    list(c(0, 0, -1), c(0, 1, 0), c(1, 0, 0)),
    list(c(0, 0, -1), c(1, 0, 0), c(0, -1, 0)),
    list(c(0, 0, 1), c(-1, 0, 0), c(0, -1, 0)),
    list(c(0, 0, 1), c(0, -1, 0), c(1, 0, 0)),
    list(c(0, 0, 1), c(0, 1, 0), c(-1, 0, 0)),
    list(c(0, 0, 1), c(1, 0, 0), c(0, 1, 0)),
    list(c(0, 1, 0), c(-1, 0, 0), c(0, 0, 1)),
    list(c(0, 1, 0), c(0, 0, -1), c(-1, 0, 0)),
    list(c(0, 1, 0), c(0, 0, 1), c(1, 0, 0)),
    list(c(0, 1, 0), c(1, 0, 0), c(0, 0, -1)),
    list(c(1, 0, 0), c(0, -1, 0), c(0, 0, -1)),
    list(c(1, 0, 0), c(0, 0, -1), c(0, 1, 0)),
    list(c(1, 0, 0), c(0, 0, 1), c(0, -1, 0)),
    list(c(1, 0, 0), c(0, 1, 0), c(0, 0, 1))
  )

  # Criar uma tabela com (x, y, z) rotacionados e um ID de rotação
  rotations |>
    purrr::map(purrr::map, `*`, point) |>
    purrr::map(purrr::map, sum) |>
    purrr::map(purrr::flatten_dbl) |>
    dplyr::tibble() |>
    purrr::set_names("point") |>
    dplyr::mutate(rotation = rotations) |>
    tibble::rowid_to_column() |>
    tidyr::unnest(point) |>
    dplyr::mutate(coord = rep(c("x", "y", "z"), dplyr::n() / 3)) |>
    tidyr::pivot_wider(names_from = coord, values_from = point) |>
    dplyr::mutate(rotation = purrr::map_chr(rotation, paste, collapse = ",")) |>
    dplyr::select(x, y, z, rotation)
}

# Fábrica de função para transformar um ponto com rotação + translação
factory_transform <- function(df) {

  # Extrair a operação de rotação da df
  rot <- df$rotation |>
    stringr::str_split("c\\(") |>
    purrr::pluck(1) |>
    stringr::str_remove("\\),?") |>
    stringr::str_subset(",") |>
    stringr::str_split(", ") |>
    purrr::map(as.numeric)

  # Extrair a operação de translação da df
  trans <- c(df$dif_x, df$dif_y, df$dif_z)

  # Retornar função que aplica a transformação
  function(vec) {
    rot |>
      purrr::map(`*`, vec) |>
      purrr::map(sum) |>
      purrr::flatten_dbl() |>
      magrittr::add(trans)
  }
}

# Pegar todas as intersecções entre detectores
get_intersections <- function(points) {

  # Parear os detectores e retornar as suas intersecções
  points |>
    purrr::map(choose_pairs) |>
    purrr::map(
      dplyr::mutate, # Intersecções são baseadas nas distâncias entre pontos
      dist = purrr::map2_dbl(a, b, ~sum((.x - .y)**2))
    ) |>
    choose_pairs() |>
    dplyr::rowwise() |>
    dplyr::group_split() |>
    purrr::map(~dplyr::inner_join(.x[["a"]][[1]], .x[["b"]][[1]], "dist")) |>
    purrr::keep(~nrow(.x) >= 66) # 66 = C(12, 2) = 12 pontos na intersec.
}

# Pegar todas as transformações que podem converter pairs1 em pairs2
get_transforms <- function(pairs1, pairs2) {

  # Criar uma função que leva pairs1[2] a pairs2[2a] ou pairs2[2b]
  dplyr::bind_rows(
    dplyr::mutate(
      apply_rotations(pairs1$a.x[[2]]),
      ref_x = pairs2$a.y[[2]][1],
      ref_y = pairs2$a.y[[2]][2],
      ref_z = pairs2$a.y[[2]][3]
    ),
    dplyr::mutate(
      apply_rotations(pairs1$a.x[[2]]),
      ref_x = pairs2$b.y[[2]][1],
      ref_y = pairs2$b.y[[2]][2],
      ref_z = pairs2$b.y[[2]][3]
    )
  ) |>
    dplyr::mutate(
      dif_x = ref_x - x,
      dif_y = ref_y - y,
      dif_z = ref_z - z
    ) |>
    dplyr::rowwise() |>
    dplyr::group_split() |>
    purrr::map(factory_transform)
}

# Encontrar a função correta de transformação
find_transform <- function(df, funs) {

  # Dadas as funções de transformação, encontrar uma que converte os pontos de
  # df (conjunto de intersecções) corretamente
  df |>
    tibble::rowid_to_column("pair_id") |>
    dplyr::rowwise() |>
    dplyr::group_split() |>
    purrr::map(~{
      .x |>
        dplyr::mutate(,
          fun_a.x = list(purrr::map(funs, ~.x(a.x[[1]]))),
          fun_id = list(seq_along(funs))
        ) |>
        tidyr::unnest(dplyr::starts_with("fun")) |>
        dplyr::select(-dist) |>
        tidyr::unnest(dplyr::everything())
    }) |>
    dplyr::bind_rows() |>
    dplyr::mutate(
      a_works = a.y == fun_a.x,
      b_works = b.y == fun_a.x
    ) |>
    dplyr::group_by(pair_id, fun_id) |>
    dplyr::summarise(
      some_works = all(a_works) || all(b_works), .groups = "drop"
    ) |>
    dplyr::ungroup() |>
    dplyr::group_by(fun_id) |>
    dplyr::summarise(works = sum(some_works)) |>
    dplyr::slice_max(works) |>
    dplyr::pull(fun_id)
}

# Ler pontos como uma lista de vetores
points <- "data-raw/19a_beacon_scanner.txt" |>
  readr::read_lines() |>
  tibble::tibble() |>
  purrr::set_names("point") |>
  dplyr::mutate(
    scanner = as.integer(stringr::str_detect(point, "scanner")),
    scanner = cumsum(scanner) - 1
  ) |>
  dplyr::filter(!stringr::str_detect(point, "scanner")) |>
  dplyr::filter(point != "") |>
  dplyr::group_split(scanner) |>
  purrr::map(dplyr::pull, point) |>
  purrr::map(purrr::map, str_to_vec)


# Reduzir detectores a uma única região
while (length(points) > 1) {

  # Pegar um par de detectores que tem uma intersecção
  pairs <- get_intersections(points)[[1]]

  # Pegar todas as funções de transformação
  funs <- get_transforms(
    dplyr::select(pairs, a.x, b.x),
    dplyr::select(pairs, a.y, b.y)
  )

  # Encontrar a função correta
  transformation <- funs[[find_transform(pairs, funs)]]

  # Converter pontos para strings
  pairs <- pairs |>
    dplyr::select(-dist) |>
    dplyr::mutate_all(purrr::map_chr, vec_to_str)

  # Criar uma cópia dos pontos que também é strings
  points_ <- purrr::map(points, purrr::map_chr, vec_to_str)

  # Encontrar detector usado como referência por transformation()
  for (i in seq_along(points_)) {

    ref <- all(c(pairs$a.y, pairs$b.y) %in% points_[[i]])
    if (ref) reference <- i
  }

  # Encontrar detector que foi transformado por transformation()
  for (i in seq_along(points_)) {

    trns <- all(c(pairs$a.x, pairs$b.x) %in% points_[[i]])
    if (trns) transformed <- i
  }

  # Aplicar transformation() em todos os pontos do detector e adicionar pontos
  # transformados ao detector de referência
  points_[[reference]] <- points[[transformed]] |>
    purrr::map(transformation) |>
    purrr::map_chr(vec_to_str) |>
    c(points_[[reference]]) |>
    unique()

  # Atualizar lista de pontos
  points_[[transformed]] <- NULL
  points <- purrr::map(points_, purrr::map, str_to_vec)
}

# Calcular o número de pontos em uma única região contígua
sum(lengths(points))
#> [1] 408

Detectores de Sinalizadores (B)

O segundo item pedia para que encontrássemos a maior distância de Manhattan entre detectores distintos.

# Reduzir detectores a uma única região, guardando as funções de tranform.
save_funs <- list()
while (length(points) > 1) {

  # Pegar um par de detectores que tem uma intersecção
  pairs <- get_intersections(points)[[1]]

  # Pegar todas as funções de transformação
  funs <- get_transforms(
    dplyr::select(pairs, a.x, b.x),
    dplyr::select(pairs, a.y, b.y)
  )

  # Encontrar a função correta
  transformation <- funs[[find_transform(pairs, funs)]]
  save_funs <- c(save_funs, transformation)

  # Converter pontos para strings
  pairs <- pairs |>
    dplyr::select(-dist) |>
    dplyr::mutate_all(purrr::map_chr, vec_to_str)

  # Criar uma cópia dos pontos que também é strings
  points_ <- purrr::map(points, purrr::map_chr, vec_to_str)

  # Encontrar detector usado como referência por transformation()
  for (i in seq_along(points_)) {

    ref <- all(c(pairs$a.y, pairs$b.y) %in% points_[[i]])
    if (ref) reference <- i
  }

  # Encontrar detector que foi transformado por transformation()
  for (i in seq_along(points_)) {

    trns <- all(c(pairs$a.x, pairs$b.x) %in% points_[[i]])
    if (trns) transformed <- i
  }

  # Aplicar transformation() em todos os pontos do detector e adicionar pontos
  # transformados ao detector de referência
  points_[[reference]] <- points[[transformed]] |>
    purrr::map(transformation) |>
    purrr::map_chr(vec_to_str) |>
    c(points_[[reference]]) |>
    unique()

  # Atualizar lista de pontos
  points_[[transformed]] <- NULL
  points <- purrr::map(points_, purrr::map, str_to_vec)
}

# Aplicar transformações aos detectores e tirar distância de Manhattan
save_funs |>
  purrr::map(~.x(c(0, 0, 0))) |>
  choose_pairs() |>
  dplyr::mutate(dist = purrr::map2_dbl(a, b, ~sum(abs(.x - .y)))) |>
  dplyr::slice_max(dist) |>
  dplyr::pull(dist)

Mapa da Fossa (A)

Depois de um domingo assustadoramente difícil, o problema do dia 20 do AoC foi bastante tranquilo de resolver. Tanto o enunciado quanto a solução me pareceram simples (apesar de algumas reclamações na internet sobre uma pegadinha que vou explicar em breve).

Hoje nós recebemos uma imagem na forma de uma matriz composta por pontos luminosos # e pontos escuros .. O outro componente da entrada era uma lista de “conversões”: nós deveríamos converter cada quadrado 3x3 da imagem em um número binário onde # = 1 e . = 0 e encontrar o elemento de índice correspondente da lista de conversões; o ponto do centro do quadrado deveria ser substituido por esse elemento da lista.

# Um quadrado 3x3
# # . . # .
# #[. . .].
# #[# . .]#
# .[. # .].
# . . # # #
#
# Número correspondente
# ...#...#. = 000100010 = 34
#
# 34o elemento da lista de conversões
# 0         10        20        30 [34]   40        50        60        70
# |         |         |         |   |     |         |         |         |
# ..#.#..#####.#.#.#.###.##.....###.##.#..###.####..#####..#....#..#..##..##

Entretanto, essa operação, denominada realce, tinha um detalhe a mais. A nossa imagem de entrada era, na verdade, infinita! Em todas as direções, a imagem deveria ser completa por infinitos pontos escuros. Nosso objetivo era contar o número de pontos luminosos que restavam na nossa imagem após 2 aplicações do realce.

Como é possível imaginar, os pontos escuros infinitos não podem fazer diferença nessa contagem (senão a resposta seria incalculável). Note que um quadrado composto só por pontos escuros equivale ao índice 0 da lista e, no exemplo acima, isso é convertido para um novo ponto escuro; ou seja, as bordas infinitas continuam sendo escuras após o realce.

A pegadinha, porém, era que a lista de conversões na entrada do problema começava com # e não ., ou seja, os infinitos pontos escuros iam virar infinitos pontos luminosos depois de um realce. Felizmente, na segunda aplicação, todos os quadrados luminosos apontariam para o 511º elemento da lista e esse sim era um .. Em conclusão, desde que aplicássemos um número par de realces, as fronteiras infinitas da imagem seriam escuras e o número de pontos luminosos poderia ser contado.

Sendo assim, o código que resolvia o problema era bem simples, bastava adicionar uma borda escura à imagem para levar em conta a fronteira infinita e seguir em frente.

# Converter uma região 3x3 em um número
img_to_int <- function(image) {

  # Achatar a matriz para uma só coluna
  bits <- ifelse(image == ".", 0, 1)
  binary <- paste0(as.vector(t(bits)), collapse = "")

  # String para inteiro
  strtoi(binary, base = 2)
}

# Aplicar realce
enhance <- function(image, algo) {

  # Iterar nas linhas e colunas, sem passar pela borda
  new_image <- image
  for (i in 2:(nrow(image) - 1)) {
    for (j in 2:(ncol(image) - 1)) {

      # Trocar [i,j] pelo índice correspondente em `algo`
      ind <- img_to_int(image[(-1:1 + i), (-1:1 + j)])
      new_image[i, j] <- algo[ind + 1]
    }
  }

  # Remover borda e retornar
  new_image[2:(nrow(image) - 1), 2:(ncol(image) - 1)]
}

# Adicionar borda
add_padding <- function(image) {

  # Adicionar mais 2 linhas em cima e embaixo
  image <- rbind(
    image[1, ], image[1, ],
    image,
    image[nrow(image), ], image[nrow(image), ]
  )

  # Adicionar 2 colunas na esquerda e na direita
  image <- cbind(
    image[, 1], image[, 1],
    image,
    image[, ncol(image)], image[, ncol(image)]
  )

  return(image)
}

# Ler lista de realce como um vetor de strings
algo <- "data-raw/20a_trench_map.txt" |>
  readr::read_lines(n_max = 1) |>
  stringr::str_split("") |>
  purrr::pluck(1)

# Ler imagem como uma matriz (e adicionar bordas)
image <- "data-raw/20a_trench_map.txt" |>
  readr::read_lines(skip = 2) |>
  purrr::prepend(rep(paste0(rep(".", 100), collapse = ""), 3)) |>
  append(rep(paste0(rep(".", 100), collapse = ""), 3)) |>
  {\(s) stringr::str_c("...", s, "...")}() |>
  stringr::str_split("") |>
  purrr::flatten_chr() |>
  matrix(106, 106, byrow = TRUE)

# Aplicar o realce duas vezes e contar pontos luminosos
image |>
  enhance(algo) |>
  add_padding() |>
  enhance(algo) |>
  magrittr::equals("#") |>
  sum()
#> [1] 5498

Mapa da Fossa (B)

O segundo item pedia apenas para aplicarmos o algoritmo 50 ao invés de 2 vezes e contar o número de pontos luminosos. Como o nosso algoritmo generaliza as bordas, podemos simplesmente aplicá-lo mais vezes.

# Aplicar o realce 50 vezes
image <- enhance(image, algo)
for (i in seq_len(49)) {
  image <- enhance(add_padding(image), algo)
}

# Contar pontos luminosos
image |>
  magrittr::equals("#") |>
  sum()
#> [1] 16014

Dados de Dirac (A)

O dia 21 do AoC começou bem. O primeiro item foi bastante direto e tranquilo… O que complicou tudo foi o segundo.

Começamos aprendendo as regras de um jogo chamado Dados de Dirac. Ele é composto um tabuleiro circular que vai de 1 a 10, um dado e dois peões para representar os dois jogadores. Cada jogador rola o dado 3 vezes, soma os resultados e anda aquele número de casas no tabuleiro; o número da casa em que ele caiu é então adicionado à pontuação do jogador. Cada jogador começa em uma casa escolhida aleatoriamente e ganha o primeiro a atingir 1000 ou mais pontos.

O primeiro item pedia para simularmos um jogo de Dados de Dirac com um dado determinístico antes de partirmos para a versão oficial. Nós recebemos como entrada a posição de início de cada jogador e a mecânica de funcionamento do dado: ele ia de 1 a 100 e seu resultado sempre vinha nessa ordem (ou seja, o primeiro jogador rolaria 1, 2, 3, o segundo rolaria 4, 5, 6, etc.). Nosso objetivo era simular o jogo até que alguém ganhasse e retornar a pontuação do jogador perdedor multiplicada pelo número de vezes que o dado foi rolado naquele jogo.

# Ler posições iniciais
pos <- "data-raw/21a_dirac_dice.txt" |>
  readr::read_lines() |>
  stringr::str_extract("[0-9]+$") |>
  as.numeric()

# Posições iniciais
p1_pos <- pos[1]
p2_pos <- pos[2]

# Pontuações iniciais
p1_pts <- 0
p2_pts <- 0

# Fazer os dados irem do valor máximo para 1
die_mod <- function(e1, e2) ((e1 - 1) %% e2) + 1

# Iterar até o jogo acabar
die <- 1
counter <- 0
while (TRUE) {

  # J1 rola 3 vezes
  p1_rolls <- die:(die + 2)
  p1_rolls <- die_mod(p1_rolls, 100)

  # Atualizar estado do dado e contador de rolagem
  die <- die_mod(p1_rolls[3] + 1, 100)
  counter <- counter + 3

  # Atualizar pontuação do J1
  p1_pos <- p1_pos + sum(p1_rolls)
  p1_pos <- die_mod(p1_pos, 10)
  p1_pts <- p1_pts + p1_pos

  # Parar se J1 ganhou
  if (p1_pts >= 1000) break

  # J2 rola 3 vezes
  p2_rolls <- die:(die + 2)
  p2_rolls <- die_mod(p2_rolls, 100)

  # Atualizar estado do dado e contador de rolagem
  die <- die_mod(p2_rolls[3] + 1, 100)
  counter <- counter + 3

  # Atualizar pontuação do J2
  p2_pos <- p2_pos + sum(p2_rolls)
  p2_pos <- die_mod(p2_pos, 10)
  p2_pts <- p2_pts + p2_pos

  # Parar se J2 ganhou
  if (p2_pts >= 1000) break
}

# Contador * pontuação do perdedor
min(p1_pts, p2_pts) * counter
#> [1] 597600

Dados de Dirac (B)

Bem direto, certo? Uma pena que o segundo item não tinha nada a ver… Agora deveríamos simular o jogo com o epônimo Dado de Dirac. Ele tem 3 lados (de 1 a 3) e, cada vez que ele é rolado, um universo paralelo é criado para cada possível resultado. Em suma, no final do jogo haveria um universo para cada caminho que o jogo poderia hipoteticamente tomar. Felizmente, com o Dado de Dirac, o jogo ia só até 21 pontos.

Nossa missão era, dadas as posições iniciais, calcular em quantos universos ganhava o jogador que ganhava mais vezes. Não parece tão difícil até você perceber que teremos algo em torno de 700 trilhões de universos para considerar. Espero que esteja claro que tentar gerar todas as rodadas não vai funcionar.

A solução ideal para esse problema é programação dinâmica (PD) que, apesar do nome esotérico, não é tão misteriosa assim. De forma bem superficial, um algoritmo que usa PD começa dividindo o problema principal em sub-problemas mais simples e armazenando seus resultados; a parte vital é, então, utilizar esses resultados já calculados para evitar contas desnecessárias mais para frente.

Concretamente, queremos dividir o jogo em estados distintos definidos pelos quartetos (p1_pos, p2_pos, p1_pts, p2_pts). Vejamos como funcionaria um trecho desse algoritmo:

Começamos por um estado no final do jogo: (3, 8, 19, 21). Neste universo, sabemos que o J2 ganhou, então salvamos a informação (3, 8, 19, 21) = (0, 1).
Mais para frente, encontramos o estado (3, 5, 19, 13). O J2 pode rolar uma série de valores aqui que precisamos verificar, mas, se ele rolar 1 + 1 + 1, sabemos que cairemos no estado (3, 8, 19, 21)! Sendo assim, podemos pular este cálculo e verificar apenas as outras rolagens possíveis.
Com PD, calcularemos primeiro estados mais fáceis e, conforme formos evoluindo para o começo do jogo, já teremos calculado o número de vitórias de cada jogador em cada futuro. Assim, basta somar esses futuros e passar para um estado anterior.

# Ler posições iniciais
pos <- "data-raw/21b_dirac_dice.txt" |>
  readr::read_lines() |>
  stringr::str_extract("[0-9]+$") |>
  as.numeric()

# Posições iniciais
p1_pos <- pos[1]
p2_pos <- pos[2]

# Fazer os dados irem do valor máximo para 1
die_mod <- function(e1, e2) ((e1 - 1) %% e2) + 1

# Criar um identificar para `states`
id <- function(a, b, c, d) paste0(a, ",", b, ",", c, ",", d)

# Contar vitórias de cada jogador a partir de cada estado do jogo
states <- list()
count_states <- function(p1_pos, p2_pos, p1_pts = 0, p2_pts = 0) {
  this_id <- id(p1_pos, p2_pos, p1_pts, p2_pts)

  # Condições de parada
  if (p1_pts >= 21) return(c(1, 0))
  if (p2_pts >= 21) return(c(0, 1))
  if (this_id %in% names(states)) return(states[[this_id]])

  # Todas as combinações possíveis de rolagens
  rolls <- list(1:3, 1:3, 1:3) |>
    purrr::cross() |>
    purrr::map(purrr::flatten_int) |>
    purrr::map_int(sum)

  # Iterar nas rolagens e fazer a recursão para os próximos estados
  wins_total <- c(0, 0)
  for (roll in rolls) {
    p1_pos_ <- die_mod(p1_pos + roll, 10)

    # Ir para o próximo estado e somar vitórias
    wins <- count_states(p2_pos, p1_pos_, p2_pts, p1_pts + p1_pos_)
    wins_total <- wins_total + rev(wins)
  }

  # Atualizar `states` e retornar
  states[[this_id]] <<- wins_total
  return(wins_total)
}

# Rodar programação dinâmica
count_states(p1_pos, p2_pos) |>
  max() |>
  format(scientific = FALSE)
#> [1] 634769613696613

Reinicialização do Reator (A)

O dia 22 do AoC foi mais um cujo enunciado não apresentou dificuldades. Não que a resolução tenha sido fácil, mas pelo menos o problema foi fácil de entender.

Essencialmente tínhamos que reiniciar o reator do submarino seguindo uma série de instruções (a entrada do problema). O reator era composto por uma grade gigantesca feita de cubos 1x1x1 que começavam todos desligados; cada instrução nos dava uma região do reator que precisava ser desligada ou ligada:

# on x=10..12,y=10..12,z=10..12
# on x=11..13,y=11..13,z=11..13
# off x=9..11,y=9..11,z=9..11
# on x=10..10,y=10..10,z=10..10

O primeiro comando da lista acima, por exemplo, ligava todos os cubos dentro da matrix reator[10:12, 10:12, 10:12]. Nosso objetivo no primeiro item era contar todos os cubos que estariam acessos no final do processo de reinicialização, mas levando em conta apenas os cubos dentro da região denotada por x=-50..50,y=-50..50,z=-50..50.

O código era bastante simples de escrever usando a função array() do R, prestando atenção apenas ao fato de que as coordenadas da array deveríam ir de 1 a 101 e não de -50 a 50.

# Ler todos os passos como uma tabela
steps <- "data-raw/22a_reactor_reboot.txt" |>
  readr::read_lines() |>
  stringr::str_split("[ ,]|(\\.\\.)") |>
  purrr::transpose() |>
  purrr::set_names("state", "x1", "x2", "y1", "y2", "z1", "z2") |>
  purrr::map(purrr::flatten_chr) |>
  tibble::as_tibble() |>
  dplyr::mutate(
    dplyr::across(dplyr::ends_with("1"), stringr::str_remove, "[a-z]="),
    dplyr::across(c(-state), as.integer),
    x = purrr::map2(x1, x2, `:`),
    y = purrr::map2(y1, y2, `:`),
    z = purrr::map2(z1, z2, `:`)
  ) |>
  dplyr::select(state, x, y, z)

# Criar reator como uma array 3D
reactor <- array(rep("off", 303), dim = c(101, 101, 101))

# Iterar nos passos
for (i in seq_len(nrow(steps))) {

  # Coordenadas do cubóide
  x <- steps$x[[i]] + 51
  y <- steps$y[[i]] + 51
  z <- steps$z[[i]] + 51

  # Eliminar o que estiver fora do cubo -50:50
  x <- x[x >= 1 & x <= 101]
  y <- y[y >= 1 & y <= 101]
  z <- z[z >= 1 & z <= 101]

  # Atribuir estado
  reactor[x, y, z] <- steps$state[i]
}

# Contar cubos ligados
sum(reactor == "on")
#> [1] 647076

Reinicialização do Reator (B)

Sem muita surpresa, o item 2 pedia para contarmos o número de cubos ligados ao final do processo de reinicialização em todo o reator. Olhando o código acima, parece que só seria necessário mudar as dimensões da array e tirar os filtros dentro do loop, certo? Infelizmente não, pois com esse algoritmo ineficiente precisaríamos contar aproximadamente 2 quadrilhões de cubos…

A solução foi, então, calcular apenas os limites das regiões e lidar com as suas intersecções. Ou seja, se dois cubóides tiverem que ser ligados, então podemos tomar nota das suas coordenadas e adicionar um novo cubóide de “subtração” na nossa lista que servirá para remover uma cópia da intersecção que foi ligada “duas vezes”. Resumidamente, estaremos contando apenas os volumes de cada cubóide ligado e subtraíndo o volume de cada intersecção para não contar nada duas vezes.

# Ler todos os passos como uma tabela
steps <- "data-raw/22b_reactor_reboot.txt" |>
  readr::read_lines() |>
  stringr::str_split("[ ,]|(\\.\\.)") |>
  purrr::transpose() |>
  purrr::set_names("state", "x1", "x2", "y1", "y2", "z1", "z2") |>
  purrr::map(purrr::flatten_chr) |>
  tibble::as_tibble() |>
  dplyr::mutate(
    dplyr::across(dplyr::ends_with("1"), stringr::str_remove, "[a-z]="),
    dplyr::across(c(-state), as.integer),
    state = ifelse(state == "on", 1L, -1L),
  )

# Iterar nos passos Iterate over steps
cuboids <- dplyr::slice_head(steps, n = 1)
for (i in 2:nrow(steps)) {

  # Iterar nos cubóides que já vimos
  for (j in seq_len(nrow(cuboids))) {

    # Calcular intersecção
    x1_inter <- max(steps$x1[i], cuboids$x1[j])
    x2_inter <- min(steps$x2[i], cuboids$x2[j])
    y1_inter <- max(steps$y1[i], cuboids$y1[j])
    y2_inter <- min(steps$y2[i], cuboids$y2[j])
    z1_inter <- max(steps$z1[i], cuboids$z1[j])
    z2_inter <- min(steps$z2[i], cuboids$z2[j])

    # Adicionar intersecção à lista (com sinal virado)
    if (x1_inter <= x2_inter && y1_inter <= y2_inter && z1_inter <= z2_inter) {
      cuboids <- tibble::add_row(cuboids,
        state = cuboids$state[j] * -1L,
        x1 = x1_inter, x2 = x2_inter,
        y1 = y1_inter, y2 = y2_inter,
        z1 = z1_inter, z2 = z2_inter,
      )
    }
  }

  # Adicionar cubóide à lista se ele estiver ligado
  if (steps$state[i] == 1) {
    cuboids <- tibble::add_row(cuboids,
      state = steps$state[i],
      x1 = steps$x1[i], x2 = steps$x2[i],
      y1 = steps$y1[i], y2 = steps$y2[i],
      z1 = steps$z1[i], z2 = steps$z2[i],
    )
  }
}

# Contar cubos ligados
on <- 0
for (i in seq_len(nrow(cuboids))) {

  # Calcular volume
  x <- cuboids$x2[i] - cuboids$x1[i] + 1
  y <- cuboids$y2[i] - cuboids$y1[i] + 1
  z <- cuboids$z2[i] - cuboids$z1[i] + 1

  # Adicionar/remover à/da conta
  on <- on + (x * y * z * cuboids$state[i])
}

# Imprimir
format(on, scientific = FALSE)
#> [1] 1233304599156793

Anfípodes (A e B)

O dia 23 do AoC foi… Estranho. O enunciado era fácil de entender, mas o código foi impossível de fazer. E não estou exagerando: eu literamente não consegui fazer o código para resolver o exercício. É verdade que eu fiquei doente hoje, então não sei se meus neurônios estavam de cama.

No meu desespero, fui olhar o subreddit do Advent em busca de sugestões de outros programadores e, quando cheguei lá, descobri que várias pessoas estavam resolvendo o problema na mão! Uma boa alma tinha até criado um helper online!

No final, a minha lição do dia de hoje é que nem sempre o jeito mais rápido de resolver um problema é programando; às vezes é mais fácil usar a cabeça mesmo. No caso, a cabeça da Renata Hirota, que resolveu o problema na mão em 10 minutos depois de eu ter passado o dia inteiro na frente do computador tentando achar uma solução.

Sendo assim, deixo vocês com uma tirinha do XKCD:

Unidade lógica e aritmética (A e B)

O penúltimo dia do AoC de 2021 chegou e, com ele, mais um problema que era mais fácil de resolver na mão! Hoje e ontem vão ficar na história como exercícios de lógica e não de programação.

Sem mais delongas, deixo vocês com outra tirinha do XKCD:

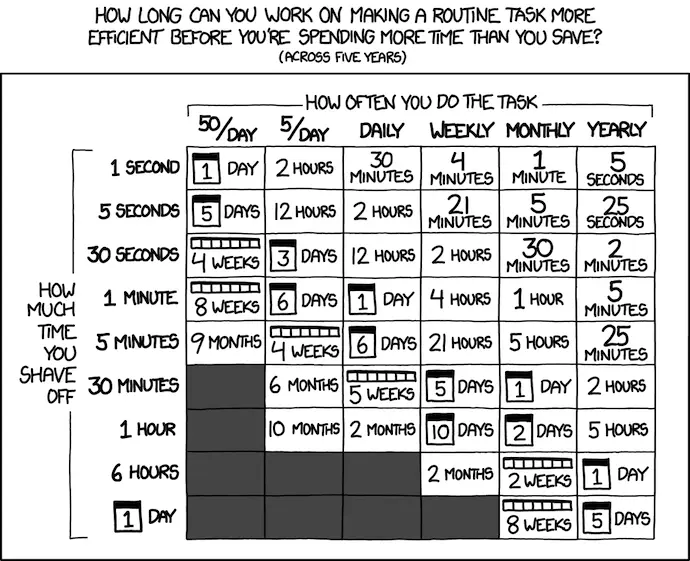
Pepino-do-mar (A)

Finalmente chegamos ao último dia do AoC deste ano! O problema de hoje foi um verdadeiro presente de Natal: bem mais simples que todos os dias anteriores. Nossa missão era acompanhar os movimentos de dois grupos de pepinos-do-mar e encontrar o momento em que eles não poderiam mais se mover.

Os pepinos estavam dispostos em uma matriz retangular e se moviam na direção para a qual estavam apontando. Se o espaço em frente ao pepino estivesse vago (.), então ele se movia.

# Estado inicial:
# ...>...
# .......
# ......>
# v.....>
# ......>
# .......
# ..vvv..
#
# Depis de 1 passo:
# ..vv>..
# .......
# >......
# v.....>
# >......
# .......
# ....v..
#
# Depois de 58 passos (todos travados):
# ..>>v>vv..
# ..v.>>vv..
# ..>>v>>vv.
# ..>>>>>vv.
# v......>vv
# v>v....>>v
# vvv.....>>
# >vv......>
# .>v.vv.v..

Meu código ficou simples. Eu li o mapa do fundo do mar como uma matriz e calculei todos os pepinos que podiam se mover; quando nenhum mais pudesse, eu retornava o número de passos transcorridos.

# Ler fundo do mar como matriz
seafloor <- "data-raw/25a_sea_cucumber.txt" |>
  readr::read_lines() |>
  stringr::str_split("") |>
  purrr::flatten_chr() |>
  matrix(nrow = 137, ncol = 139, byrow = TRUE)

# Iterar enquanto ainda há movimentos
i <- 0
while (TRUE) {
  i <- i + 1

  # Todos os pepinos
  e <- which(seafloor == ">")
  s <- which(seafloor == "v")

  # As suas próximas posições
  next_e <- ((e + 137) %% 19043) + ((e + 137) %% 19043 == 0) * 19043
  next_s <- s + 1 - (s %% 137 == 0) * 137

  # Mover todos os pepinos virados para a esquerda
  allowed_e <- seafloor[next_e] == "."
  seafloor[next_e[allowed_e]] <- seafloor[e[allowed_e]]
  seafloor[e[allowed_e]] <- "."

  # Mover todos os pepinos virados para baixo
  allowed_s <- seafloor[next_s] == "."
  seafloor[next_s[allowed_s]] <- seafloor[s[allowed_s]]
  seafloor[s[allowed_s]] <- "."

  # Verificar condição de parada
  if (all(!allowed_e) && all(!allowed_s)) break
}

# Imprimir
print(i)
#> [1] 518

Pepino-do-mar (B)

O segundo item me pegou de surpresa porque… Não havia segundo item! A historinha que estava sendo contada ao longo do AoC foi finalmente concluída e ganhamos a última estrela de graça.

E esse foi o fim da aventura. Muito obrigado por me acompanhar nesses últimos 25 dias de programação intensa! Espero que tenham gostado e, até que enfim, boas festas!

#r #aoc #cs

Responda a este post por email ↪