Rolando dados com droll
droll [ˈdrōl] (adj.). 1. (Ing.) Divertido, especialmente de forma incomum.
droll é um pacote R para parsear a notação usada para descrever dados, analisar rolagens, calcular probabilidades de sucesso e gerar gráficos das distribuições dos resultados. Ele pode ajudar DMs detalhistas a preparar encontros (in)justos com antecedência ou decidir a DC apropriada para um teste na hora. Jogadores também podem usar o droll para determinar a melhor estratégia quando em uma situação difícil.
Ele foi feito para ser uma alternativa muito leve (só uma dependência obrigatória), muito rápida (menos de 0,4s para calcular a distribuição completa de 40d6) e muito precisa (representação interna simbólica cortesia do Ryacas) para o anydice no R.
Instalação
Instale a versão estável do CRAN com:
install.packages("droll")Ou instale a versão em desenvolvimento do GitHub com:
# install.packages("remotes")
remotes::install_github("curso-r/droll")Uso
O que você procura no droll? Você é um usuário nível 1, um programador experiente nível 10, ou um estatístico divino nível 20? Escolha sua classe:
🖍️ Usuário
O uso mais básico do droll envolve simplesmente rolar dados. Você pode
criar qualquer dado que quiser com a função d() e escrever qualquer
expressão que envolva aquele dado. Note que, se você quiser rolar NdX,
você deveria escrever N * dX.
# Criar alguns dados
d20 <- d(20)
d6 <- d(6)
d4 <- d(4)
# Rolar um teste enquanto abençoado
(d20 + 8) + d4
#> [1] 22
# Rolar o dano!!
8 * d6
#> [1] 22
# Rolar um teste de resistência de destreza com desvantagem
if (min(d20, d20) + 4 < 18) {
print("Dano completo!")
} else {
print("Metade do dano.")
}
#> [1] "Dano completo!"Simples e fácil, certo? Se você é um DM, você também pode querer usar
duas funções: check_prob() e check_dc(). Elas permitem que você,
respectivamente, calcule a probabilidade de passar (ou falhar) em um
teste e encontrar a DC necessária para que um teste tenha uma certa
probabilidade de sucesso (ou erro). Você não precisa nem criar os dados
que você vai usar dentro delas!
# Qual é a probabilidade que esse jogador passe em um teste de DC 15?
check_prob(d20 + 8, 15)
#> [1] 0.7
# Qual deveria ser a DC para que esse jogador tenha 50% de chance de sucesso?
check_dc(d20 + 8, 0.5)
#> [1] 19
# Qual é a probabilidade desse jogador falhar em um teste de DC 10?
check_prob(d20 + 8, 10, success = FALSE)
#> [1] 0.05
# Qual deveria ser a DC para que esse jogador tenha 90% de chance de falha?
check_dc(d20 + 8, 0.9, success = FALSE)
#> [1] 27Não há funções do tipo attack_*() porque as mecânicas de ataques e
testes são as mesmas, ou seja, sucesso equivale a rolar um valor maior
ou igual a um certo patamar. Essas funções podem, portanto, ser usadas
para ataques também!
🗡️ Programador
Se você já está acostumado com a notação d/p/q/r do R, pode ser que você
queira mais detalhes sobre a distribuição de uma rolagem. É para isso
que as funções droll(), proll(), qroll(), e rroll() existem!
Elas são, respectivamente, a densidade, a função de distribuição, a
função de quantil, e a geração aleatória da distribuição definida por
uma expressão de rolagem.
# P[d20 + 8 = 12]
droll(12, d20 + 8)
#> [1] 0.05
# P[d20 + 8 <= 12]
proll(12, d20 + 8)
#> [1] 0.2
# inf{x: P[d20 + 8 <= x] >= 0.5}
qroll(0.5, d20 + 8)
#> [1] 18
# Amostrar 3 vezes de d20 + 8
rroll(3, d20 + 8)
#> [1] 16 26 9Quando você aprender a usar essas quatro funções, você pode olhar as
suas variações plot_*() delas. Elas geram gráficos (usando o ggplot2
se ele estiver disponível) correspondendo às distribuições completas de
d/p/q e um histograma simples no caso da plot_rroll().
# Densidade de 8d6
droll_plot(8 * d6)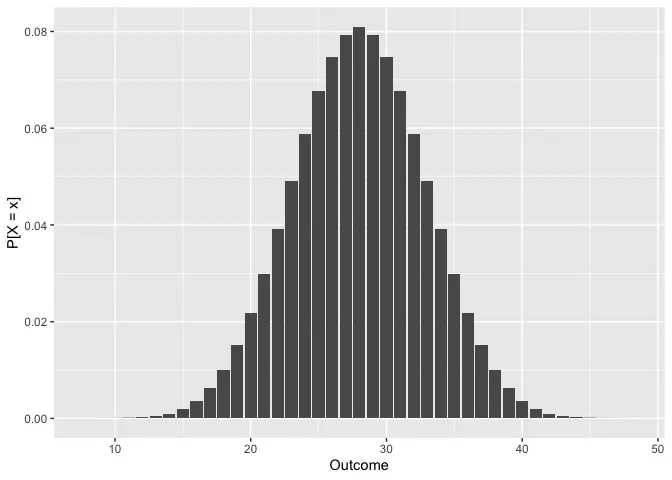
# Função de distribuição de 8d6
proll_plot(8 * d6)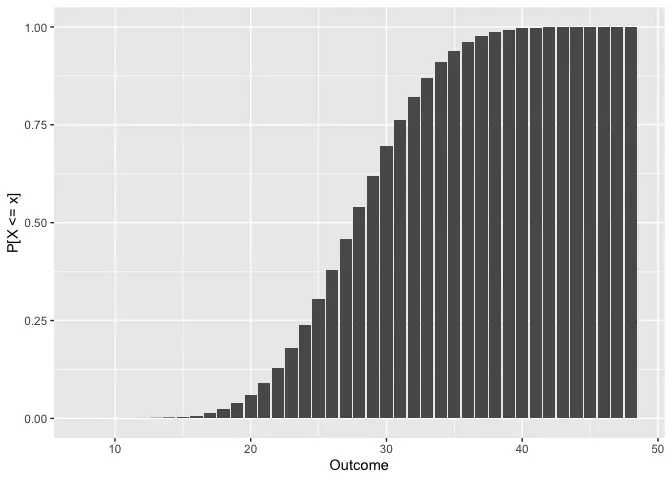
# Função de quantil de 8d6
qroll_plot(8 * d6)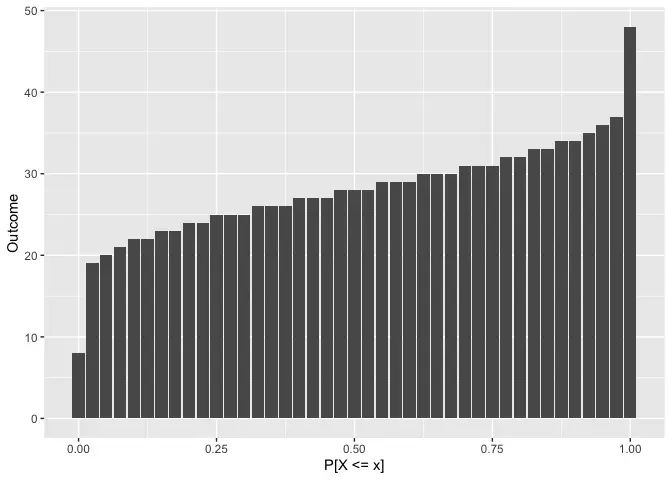
# Histograma de 1000 rolagens de 8d6
rroll_plot(1000, 8 * d6)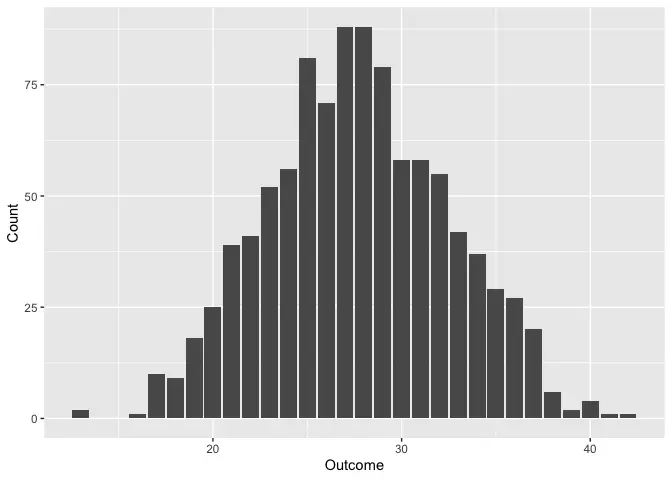
Toda função p/q também tem um conveniente argumento lower.tail que
pode ser igual a FALSE para que os cálculos sejam feitos a partir da
cauda superior da distribuição.
🪄 Estatístico
Já que você é um veterano do R, você precisa ser capaz de dobrar o droll
à sua vontade. Se você gostaria de ver o tecido da realidade do droll,
você pode usar a função r() para obter uma distribuição de rolagem
completa. Se você quiser precisão máxima, você também pode impedir o
droll de converter a sua representação interna (operada pelo Ryacas)
para doubles com precise = TRUE.
# Obter a distribuição completa de 8d6
r(8 * d6)
#> # A tibble: 41 × 4
#> outcome n d p
#> <dbl> <dbl> <dbl> <dbl>
#> 1 8 1 0.000000595 0.000000595
#> 2 9 8 0.00000476 0.00000536
#> 3 10 36 0.0000214 0.0000268
#> 4 11 120 0.0000714 0.0000982
#> 5 12 330 0.000196 0.000295
#> 6 13 792 0.000472 0.000766
#> 7 14 1708 0.00102 0.00178
#> 8 15 3368 0.00201 0.00379
#> 9 16 6147 0.00366 0.00745
#> 10 17 10480 0.00624 0.0137
#> # … with 31 more rows
# Poder ilimitado
r(8 * d6, precise = TRUE)
#> # A tibble: 41 × 4
#> outcome n d p
#> <dbl> <chr> <chr> <chr>
#> 1 8 1 1/1679616 1/1679616
#> 2 9 8 1/209952 1/186624
#> 3 10 36 1/46656 5/186624
#> 4 11 120 5/69984 55/559872
#> 5 12 330 55/279936 55/186624
#> 6 13 792 11/23328 143/186624
#> 7 14 1708 427/419904 2995/1679616
#> 8 15 3368 421/209952 707/186624
#> 9 16 6147 683/186624 695/93312
#> 10 17 10480 655/104976 11495/839808
#> # … with 31 more rowsA tabela retornada por r() pode ser usada no lugar do argumento roll
de todas as funções discutidas acima. Isso pula os cálculos internos, um
atalho valioso se você quiser rodar múltiplos diagnósticos para a mesma
expressão de rolagem.
Como um estatístico nível 20, você também não está limitado pelos dados
internos do droll. Você pode criar dados personalizados usando a mesma
função d() descrita anteriormente.
# Criar um dado "fudge"
dF <- d(-1:1)
rroll(5, dF)
#> [1] -1 1 1 -1 -1
# Criar um 2d20kh, um "dado de vantagem"
df <- r(max(d20, d20))
kh <- d(rep(df$outcome, df$n))
rroll(5, kh)
#> [1] 12 5 9 5 18