Uma Bela Herança

O motivador da discussão deste post é meio estranho: em 17 de dezembro de 2020 serão comemorados 250 anos desde o nascimento do grande compositor alemão Ludwig van Beethoven. Não é incomum ver pessoas abrindo poupanças para seus filhos logo quando nascem (para que eles tenham um pé-de-meia quando crescerem) e isso me fez pensar como ficaria uma poupança aberta para Beethoven 250 anos atrás…

Sendo assim, em pleno 2020, uma carta chega à casa do último herdeiro vivo do músico, você, lhe dando acesso à recém-descoberta poupança do seu tatara-tataravô. Como poderia existir uma poupança em 17 de dezembro de 1770 ou como ela durou até hoje é um mistério, mas sabe-se que ela foi aberta com o que atualmente seriam R$ 500,00.

Visualizando a Poupança

Para saber quanto dinheiro há hoje na poupança, basta utilizar a fórmula de juros compostos: $V_f=V_p(1+j{)}^n$ . Aqui $V_f$ é o valor final, $V_p$ é o valor inicial, $j$ é a taxa de juros e $n$ é o número de períodos que o dinheiro ficou guardado (número de anos se os juros forem anuais, número de meses se os juros forem mensais, etc.).

Mas, muito mais do que simplesmente obter o valor final, é interessante ver o crescimento dos fundos da poupança ao longo do tempo. Isso pode ser feito com o pacote ggplot2 facilmente: basta utilizar a fórmula acima para cada um dos 250 anos e plotar esses pontos em um scatterplot. Entretanto, temos uma opção ainda melhor.

Um recurso pouco conhecido do ggplot2 é o stat_function(), capaz de construir uma linha contínua no gráfico a partir de uma função que recebe o valor de uma abscissa e retorna o valor da ordenada correspondente. Ou seja, se tivermos uma função f(x) = y, podemos passá-la como argumento para o stat_function() desenhá-la (com o nível de resolução mais apropriado).

Sendo assim, precisamos transformar a função ternária Vp*(1+j)**n em uma função que recebe apenas um argumento. Para isso devemos usar uma técnica denominada currying, que essencialmente “pré-preenche” argumentos de uma função; nesse caso, vamos fixar o valor de Vp e j de modo que somente o n varie. A função unária final, que podemos construir com purrr::partial(), nos mostrará quanto tinha na poupança depois de n unidades de tempo (a saber, anos).

O código final para a visualização é o seguinte:

library(magrittr)

# Fórmula de juros compostos
juro_composto <- function(Vp, j, n) Vp*(1+j)**n

# Gerar um gráfico de juros compostos
grafico_juros <- function(Vp, j, n, SI = TRUE) {

  # Atalho para o ggplot (currying)
  juro_fixado <- purrr::partial(juro_composto, Vp = Vp, j = j)

  # Exibir eixos de forma abreviada
  scale_real <- if (SI) { scales::label_number_si(prefix = "R$ ") } else { I }

  # Mostrar no gráfico
  c(0, n) %>%
    dplyr::tibble(x = .) %>%
    ggplot2::ggplot(ggplot2::aes(x)) +
    ggplot2::stat_function(fun = juro_fixado) +
    ggplot2::scale_y_continuous(labels = scale_real) +
    ggplot2::xlab("Anos") +
    ggplot2::ylab("Valor Final") +
    ggplot2::theme_minimal()
}

Agora vamos para os detalhes da poupança. Para desconsiderarmos a inflação, digamos que a poupança começou com o que nos valores de hoje seriam R$ 500,00; uma poupança rende, em média, módicos 6% ao ano, então vamos usar isso como referência; por fim, o dinheiro ficou parado lá por 250 anos. Quanto você acha que terá na conta agora em 2020?

grafico_juros(500, 0.06, 250)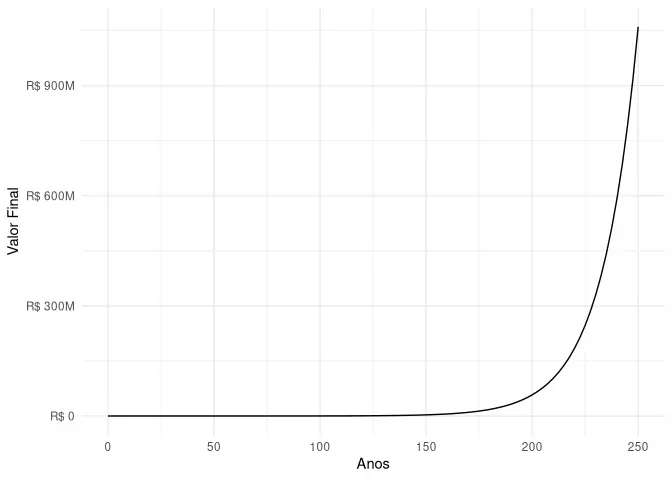

Como é de se esperar, juros compostos são uma função exponencial. Depois desses 250 anos, os R$ 500,00 se tornaram mais de R$ 1B. Nada mal para uma mera poupança.

Bônus

Aproveitando que já temos todo o código pronto, podemos visualizar outras séries exponenciais. Se colocássemos 1 centavo na poupança no ano 1 D.C., hoje em dia teríamos aproximadamente R$ 1.3e+49, ou mais ou menos R$ 0,10 para cada átomo da Terra. Essa é a mágica dos juros compostos.

grafico_juros(0.01, 0.06, 2020, FALSE)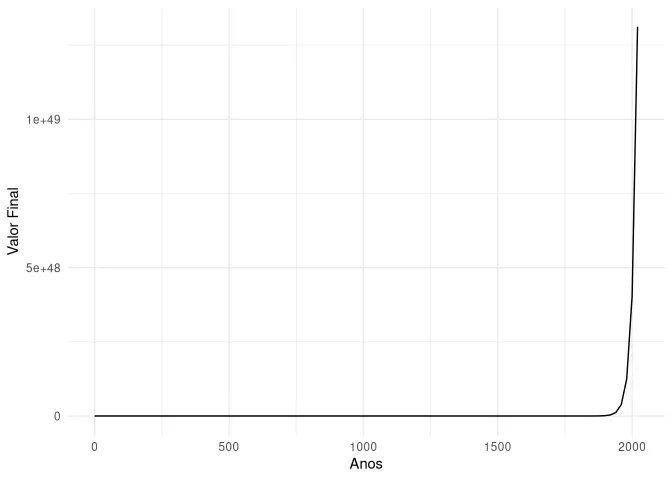

Uma propriedade interessante de frases como “crescimento de 3%” é que raramente notamos que essa porcentagem se acumula ano-a-ano. Um país cujo PIB cresce 3% ao ano tem que dobrar a sua economia a cada 25 anos. Atualmente o PIB do Brasil é de R$ 7T, vejamos o gráfico de nossa economia crescendo a 3% todo ano:

grafico_juros(7e12, 0.03, 25)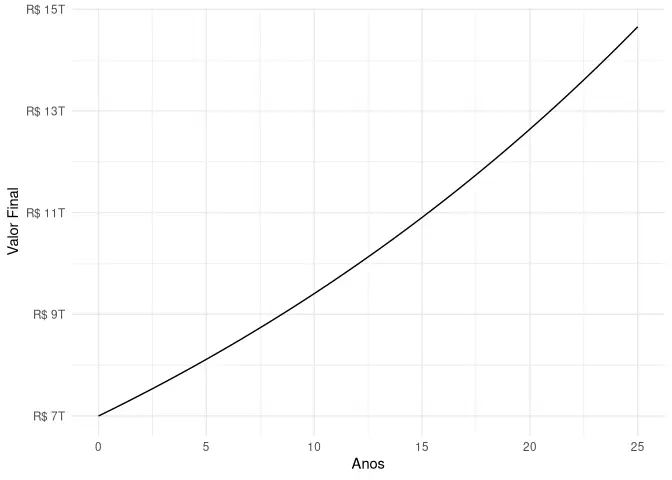

Isso pode não impressionar muito, mas, se começarmos a falar em escalas globais, a coisa muda de figura. Os EUA têm um PIB de US$ 17T, enquanto a soma de todos os PIBs do mundo dá aproximadamente US$ 80T; se a economia estadunidense crescesse a 3% pelos próximos 100 anos, precisaríamos de mais de 4 PIBs mundiais para chegar perto desse novo PIB dos EUA.

grafico_juros(17e12, 0.03, 100)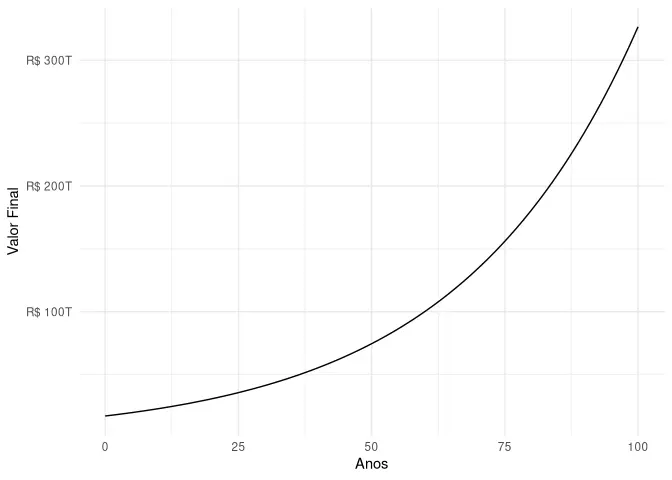

Uma coisa que não cresce exponencialmente, entretanto, é a quantidade de recursos disponíveis na natureza…